多头注意力是什么
什么是多头注意力
在上一篇文章里面我们已经讲完了 Self Attention|自注意力,这里我们在自注意力的基础上多增加一点东西:加上多头注意力(Multi-Head Attention,MHA)。这个其实才是本来 Transformer 的自注意力的完全版本1。因为大部分内容在前文已经讲完,本篇不会太长~
之前我们提到有下面这三个矩阵
$$ \mathbf Q,\mathbf K,\mathbf V\in\mathcal{R}^{n\times d} $$
假设有 $n_h$ 个头,多头注意力的意思就是将每个长度为 $d$ 的 Query/Key/Value 向量切分为 $n_h$ 个,所以每一个头的向量长度变成了 $d_h=d/n_h$,那么上面 3 个矩阵就变成了
$$ \mathbf Q,\mathbf K,\mathbf V\in\mathcal{R}^{n_h\times n\times d_h} $$
注意在维度里面,$n_h$ 放在第一个位置
为啥要这样子做呢?可以从矩阵乘法的角度入手。在不采用多头注意力之前
$$ \begin{split} \mathbf Q\in\mathcal{R}^{n\times d}\\ \mathbf K^T\in\mathcal{R}^{d\times n}\\ \mathbf Q\mathbf K^T\in\mathcal R^{n\times n} \end{split} $$
我们得到了一个注意力分数矩阵
在采用多头注意力之后,维度变成了如下的样子
$$ \begin{split} \mathbf Q\in\mathcal{R}^{n_h\times n\times d_h}\\ \mathbf K^T\in\mathcal{R}^{n_h\times d_h\times n}\\ \mathbf Q\mathbf K^T\in\mathcal R^{n_h\times n\times n} \end{split} $$
我们得到了 $n_h$ 个注意力分数矩阵。同样的,我还是用 Exclidraw 画了一张图来示意(假设 $n_h=4$),相同颜色之间进行运算,4 种颜色所以得到了 4 套注意力分数矩阵
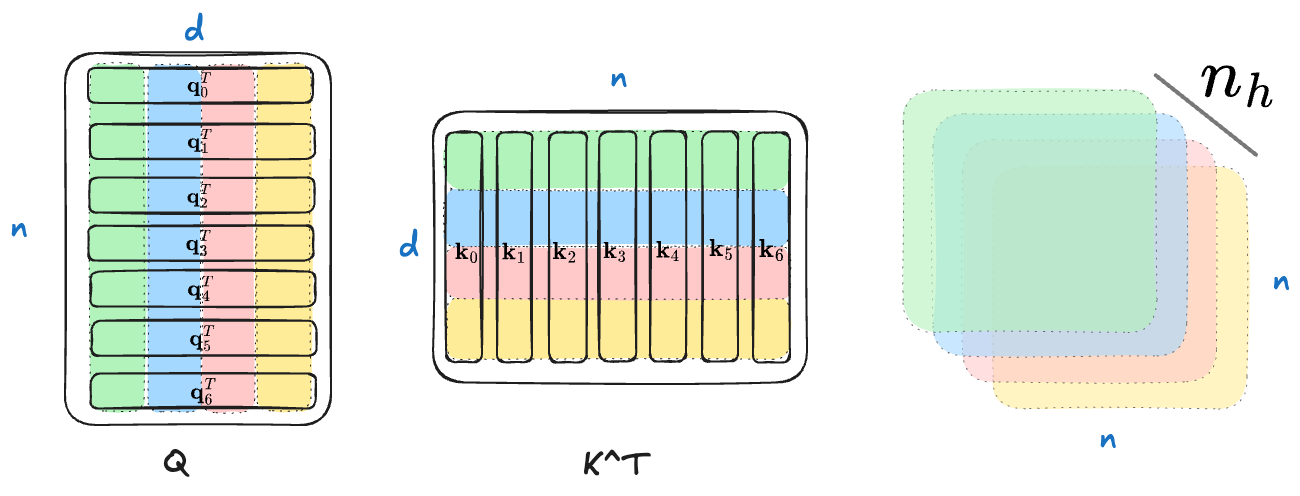
为了公式的简洁,忽略用 $1/\sqrt d_h$ 做 Scaling,那么多头注意力最后的输出是
$$ \texttt{softmax}(\mathbf Q\mathbf K^T)\mathbf V\in\mathcal R^{n_h\times n\times d_h} $$
最后做一下 reshape,将 $\mathcal R^{n_h\times n\times d_h}$ 变回 $\mathcal{R}^{n\times d}$ 即可
实现多头注意力
基于之前自注意力的代码,进行如下的操作就可以得到多头注意力
- 实现单向注意力矩阵的
bias需要的目标维度是(1, 1, block_size, block_size) q, k, v都需要 reshape 一下- 最后做
attn @ v需要调用contiguous然后再做 Reshape
完整代码在这里
class MultiHeadAttn(nn.Module):
def __init__(self, n_embd: int, block_size: int, n_heads: int):
super().__init__()
self.attn = nn.Linear(n_embd, 3 * n_embd)
self.n_embd = n_embd
self.n_heads = n_heads
assert self.n_embd % self.n_heads == 0
self.register_buffer(
"bias",
torch.tril(torch.ones(block_size, block_size)).view(
1,
1,
block_size,
block_size,
),
)
def forward(self, x):
B, T, C = x.size() # (batch_size, seq_len, n_embd)
qkv = self.attn(x) # qkv: (batch_size, seq_len, 3 * n_embd)
q, k, v = qkv.split(self.n_embd, dim=2) # split in n_embd dimension
q = q.view(B, T, self.n_heads, C // self.n_heads).transpose(
1, 2
) # q: (batch_size, n_heads, seq_len, n_embd)
k = k.view(B, T, self.n_heads, C // self.n_heads).transpose(
1, 2
) # k: (batch_size, n_heads, seq_len, n_embd)
v = v.view(B, T, self.n_heads, C // self.n_heads).transpose(
1, 2
) # v: (batch_size, n_heads, seq_len, n_embd)
attn = (q @ k.transpose(-2, -1)) * (
1.0 / math.sqrt(k.size(-1))
) # attn: (batch_size, n_heads, seq_len, seq_len)
attn = attn.masked_fill(self.bias[:, :, :T, :T] == 0, -float("inf"))
attn = F.softmax(attn, dim=-1)
out = (attn @ v).transpose(1, 2).contiguous().view(B, T, C)
return out总结
总结来说,多头注意力的奥妙就在维度上。通过多头注意力,虽然 Query/Key/Value 向量都变短了($d\rightarrow d_h$),但是我们得到了更多的注意力分数矩阵($1\rightarrow n_h$)。如果说每一个注意力分数矩阵都捕捉了一种模式的话,那么多头注意力就是捕捉了多种模式,那效果自然就更好了 :)