如何理解 Transformer 的自注意力公式

引言

大模型基于 Transformer 架构搭建而成，而自注意力机制是 Transformer 的核心。要理解大模型就要从理解自注意力开始。在本篇文章里，我将拆解自注意力公式来帮助你理解，最后还会手撕自注意力的 PyTorch 代码 :0

自注意力的理解

在原论文里面，自注意力的公式是¹

$$ \texttt{Self-Attention}(\mathbf Q, \mathbf K, \mathbf V)=\texttt{softmax}(\frac{\mathbf Q\mathbf K^T}{\sqrt d})\mathbf V $$

上面是公式描述，如果看不懂也没关系，后面会逐步拆解。简单来说，自注意力的原理是：对于每个 token $i$，通过计算得到它的 Query ($\mathbf q_i$)、Key ($\mathbf k_i$)、Value ($\mathbf v_i)$ 向量，然后这个 token $i$ 会拿着它自己的 $\mathbf q_i$ 和其他所有的 （包括 token $i$ 自己）token 的 $\mathbf k_j$ 向量计算注意力分数 $a_{ij}$，每个 $(\texttt{token } i,\texttt{token } j)$ 的 pair 都可以得到注意力分数 $a_{ij}$，每个注意力分数 $a_{ij}$ 都会和对应的 $\mathbf v_j$ 相乘，这样子做加权和之后就得到了 token $i$ 的新的向量表示

这么说可能有点绕，因此下面来拆解一下上面的公式，这个公式里面涉及到这么几个变量 $\mathbf Q,\mathbf K,\mathbf V,d_k$，他们的意思分别是

• $\mathbf Q$ 表示所有 token 的 Query 向量构成的矩阵
• $\mathbf K$ 表示所有 token 的 Key 向量构成的矩阵
• $\mathbf V$ 表示所有 token 的 Value 向量构成的矩阵
• $d$ 表示 Query/Key/Value 向量的长度

首先需要知道怎么从输入得到 $\mathbf Q,\mathbf K,\mathbf V$。用 $\mathbf x_{1:n}$ 表示输入的 $n$ 个 token 的向量表示，通过 $\mathbf W^Q, \mathbf W^K, \mathbf W^V$ 三个矩阵的权重变换（其实就是 矩阵乘法）就得到 $\mathbf Q,\mathbf K, \mathbf V$

$$ \mathbf Q,\mathbf K,\mathbf V\in\mathcal{R}^{n\times d} $$

我用 Exclidraw 画了一张图，来帮助你进行理解这 3 个矩阵

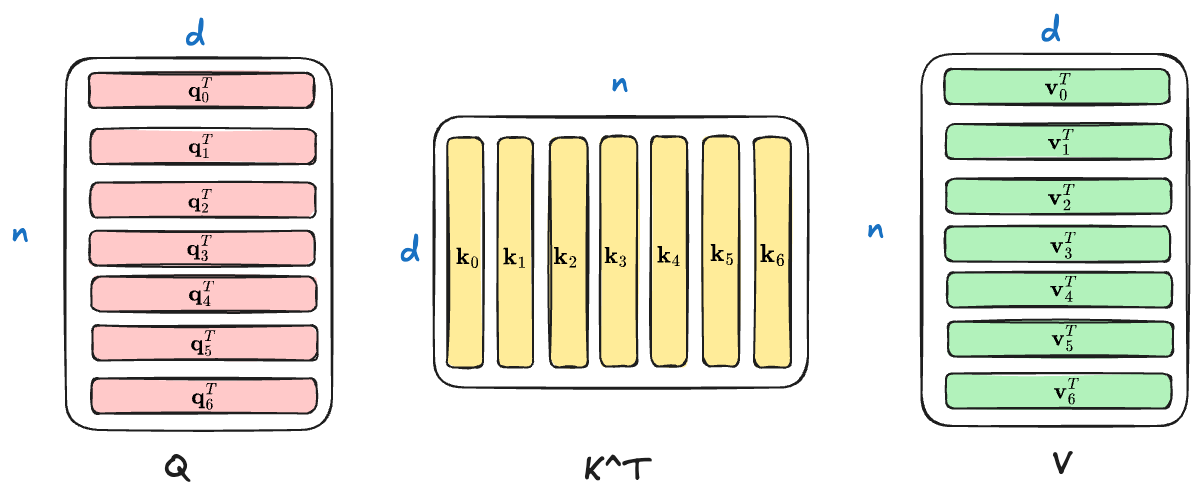
先看自注意力公式的核心部分

$$ \mathbf Q\mathbf K^T\in\mathcal R^{n\times n} $$

$\mathbf Q\mathbf K^T$ 得到的是一个 $n\times n$ 的矩阵（这里 $n$ 是输入的长度），其中位置 $(i, j)$ 表示 $\mathbf q_i^T\mathbf k_j$ 这个向量内积，这就是 token $i$ 和 token $j$ 的注意力分数。所以 $\mathbf Q\mathbf K^T$ 就是一个 token-to-token 的注意力分数矩阵。以 $\mathbf q_0$ 为例，它和所有 token 的 $k_j$ 向量的注意力分数的计算可以用下图进行描述

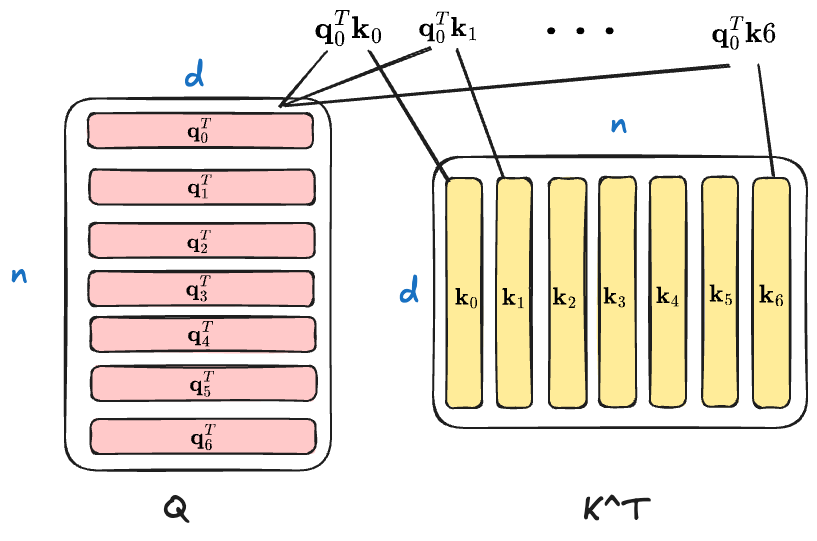
接下来是在注意力矩阵上加 $\texttt{softmax}$ 做归一化，确保注意力分数矩阵的每一行的注意力分数的和为 1

$$ \texttt{softmax}(\mathbf Q\mathbf K^T)\in\mathcal R^{n\times n} $$

最后，将归一化后的注意力分数矩阵乘以 $\mathbf V$

$$ \texttt{softmax}(\mathbf Q\mathbf K^T)\mathbf V\in\mathcal R^{n\times d} $$

这就是前面所说的加权和，比如我们考虑 token $0$，它和所有 token $j$ 的注意力分数是

$$ [\mathbf q_0^T\mathbf k_0, \mathbf q_0^T\mathbf k_1, \mathbf q_0^T\mathbf k_2, …, \mathbf q_0^T\mathbf k_j]=[a_{00}, a_{01}, …,a_{0j}] $$

做加权和会得到

$$ \sum_j(\mathbf q_0^T\mathbf k_j)\mathbf v_j=\sum_j a_{0j}\mathbf v_j $$

如下图所示

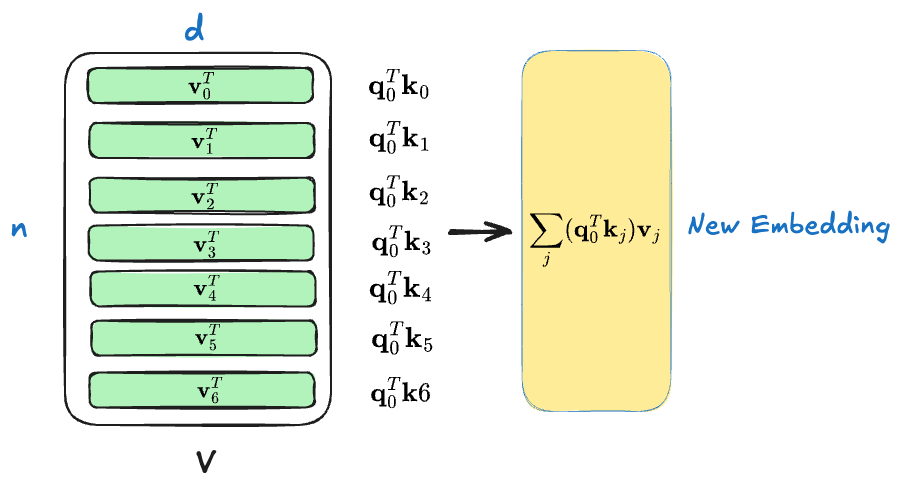
这就是 token $0$ 更新后的向量表示，其他的 token 同理

现在只剩下最后一个问题，为什么要除以一个 $\sqrt{d}$？其实在原论文里就有答案 ¹：作者说在计算注意力的时候 $\mathbf q_i^T\mathbf k$ 的向量内积可能会很大，这样会导致被 $\texttt{softmax}$ 之后落在“饱和区”，梯度会比较小，就不利于用 Gradient-descent|梯度下降 算法优化。所以用 $1/\sqrt d$ 做一下 Scaling

这里的 $\sqrt d$ 其实是 L2 范数，比如向量 $[1, 1]$ 长度为 2，L2 范数 就是 $\sqrt 2$，那么长度为 $d$ 的向量的 L2 范数 就是 $\sqrt d$ 了

自注意力实现

上面讲述了自注意力的原理，下面就来手撕一下自注意力算法的代码，注意实现的时候会做一些优化，比如

• $\mathbf W^Q, \mathbf W^K, \mathbf W^V$ 没有必要用 3 个 nn.Linear，直接用 1 个 nn.Linear 然后做 split 就行
• 实现单向注意力只需要在计算出 $\mathbf Q\mathbf K^T$ 之后，将不需要做注意力运算（上三角部分）的位置赋值为 -float('inf')，那么在 $\texttt{softmax}$ 之后这些位置的注意力自然就是 0 了

总结上面的说明，可以得到下面的代码（我添加了注释）

import math
import torch
import torch.nn as nn
import torch.nn.functional as F

class NaiveAttention(nn.Module):
    def __init__(self, n_embd: int, block_size: int):
        super().__init__()
        self.attn = nn.Linear(n_embd, 3 * n_embd)
        self.n_embd = n_embd
        self.register_buffer(
            "bias",
            torch.tril(torch.ones(block_size, block_size)).view(
                1,
                block_size,
                block_size,
            ),
        )

    def forward(self, x):
        B, T, C = x.size()  # (batch_size, seq_len, n_embd)
        qkv = self.attn(x)  # qkv: (batch_size, seq_len, 3 * n_embd)
        q, k, v = qkv.split(self.n_embd, dim=2)  # split in n_embd dimension
        attn = (q @ k.transpose(1, 2)) * (
            1.0 / math.sqrt(k.size(-1))
        )  # attn: (batch_size, seq_len, seq_len)
        attn = attn.masked_fill(self.bias[:, :T, :T] == 0, -float("inf"))
        attn = F.softmax(attn, dim=-1)
        # print(f"{attn=}")
        out = attn @ v  # (batch_size, seq_len, n_embd)

        return out

然后可以随便构造一个输入

module = NaiveAttention(n_embd=4, block_size=5)
sample_input = torch.randn(1, 5, 4)

查看一下注意力分数矩阵（即 attn 变量）和最后的输出（即 out 变量）

# attn matrix:
[[[1.0000, 0.0000, 0.0000, 0.0000, 0.0000],
  [0.3017, 0.6983, 0.0000, 0.0000, 0.0000],
  [0.3125, 0.2572, 0.4303, 0.0000, 0.0000],
  [0.2190, 0.3706, 0.2354, 0.1750, 0.0000],
  [0.1901, 0.2321, 0.1831, 0.1889, 0.2058]]]

# output:
[[[0.2348, 0.0224, 0.5836, 0.1414],
  [0.1057, 0.2104, 0.6170, 0.5556],
  [0.4593, 0.0303, 0.7982, 0.0422],
  [0.2862, 0.1033, 0.6313, 0.2689],
  [0.3003, 0.1009, 0.6536, 0.2153]]]

总结

以上就是本文的所有内容，本文的目的是让你对 Transformer 的自注意力机制有一个基本的了解。当然这并不是现如今大模型用的自注意力版本。在此之上，还有多头注意力（MHA）、多头潜在注意力（MLA）等，这些打算放到后续的文章讲解 : )

Ref