反向传播公式推导和理解

更新：矩阵形式的反向传播可以看 这里

引言

在深度学习中，模型的优化是通过采用梯度下降法不断更新权重和偏置项，让损失越来越小。其中的核心就是反向传播算法。回忆梯度下降的公式，用 $\theta$ 表示模型所有可学习的参数，$J$ 表示损失函数，$\alpha$ 表示学习率，那么有

$$ \theta \leftarrow \theta - \alpha * \frac{\partial J}{\partial \theta} $$

反向传播要求解的就是上面式子中 $\frac{\partial J}{\partial \theta}$ 这一项。只有正确高效计算出梯度，模型才可以沿着梯度的负方向更新不断优化。

📒 本文会交叉使用「参数」和「权重和偏置项」这两个术语，他们是同一个意思，都表示了模型可以学习的参数

📒 本文假定你对数学上的求导链式法则等有所了解🫡

模型假设

本文要讲解反向传播，那么当然要定义一个模型用于之后的推导，考虑一个简单然而很经典的三层全连接层，如下所示:

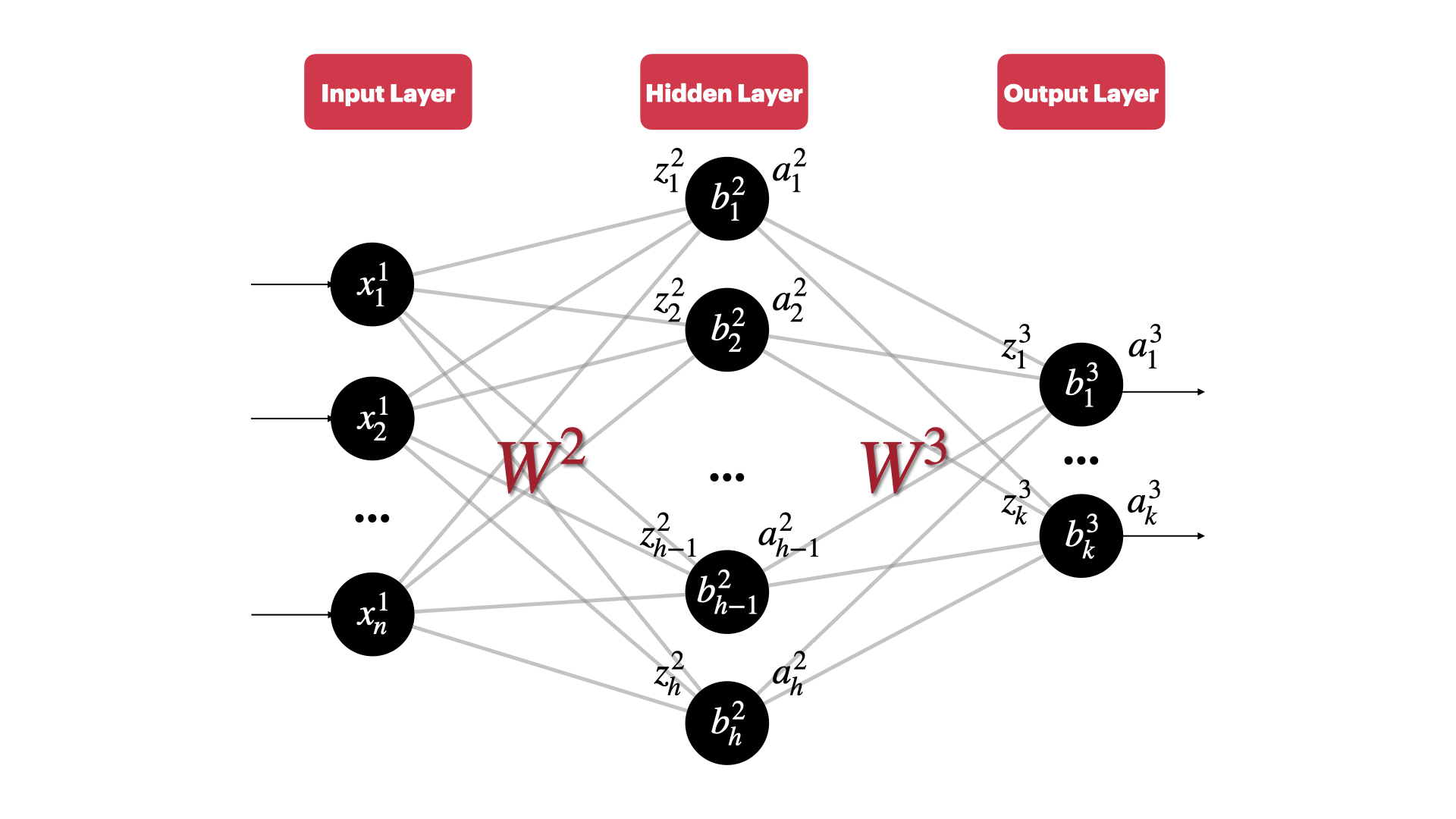
📒 为了记号方便，大写字母表示矩阵，小写字母表示向量（无下标）或者标量（有下标）

并规定如下记号：

• 不同层的神经元个数：输入层有 $n$ 个神经元，隐藏层有 $h$ 个神经元，输出层有 $k$ 个神经元
• $x^1_j$ 表示输入的第 $j$ 个特征。记输入层第 $1$ 层
• $y_j$ 表示对应输出层的第 $j$ 个输出的真实值
• $w^l_{jk}$ 表示第 $l-1$ 层的第 $k$ 个神经元和第 $l$ 层的第 $j$ 个神经元这个链接对应的权重，注意这里的下角标是从后面指向前面。根据前面的隐藏层大小，可以算出权重矩阵的大小为：
  • $W^2\in \mathcal{R}^{h\times n}$
  • $W^3\in \mathcal{R}^{k\times h}$
• $b_j^l$ 表示第 $l$ 层的第 $j$ 个神经元的偏置项
• $z_j^l$ 表示第 $l$ 层的第 $j$ 个神经元计算的加权和
• $a_j^l$ 表示第 $l$ 层的第 $j$ 个神经元的激活函数输出值

根据上面的记号，模型的前向传播的公式如下：

$$ z_j^2 = \sum_kw_{jk}^2x^1_k+b_j^2 $$

$$ a_j^2=\sigma(z_j^2) $$

$$ z_j^3 = \sum_kw_{jk}^3a_k^2+b_j^3 $$

$$ a_j^3=\sigma(z_j^3) $$

更一般的，可以对上面的公式进行概括。$z_j^l$ 和 $a_j^l$ 的计算方式如下： $$ z_j^l=\sum_kw_{jk}^la^{l-1}_k+b_j^l $$

$$ a_j^l=\sigma(z_j^l) $$

上面这两个公式很重要，特别要弄清楚式子的下标和上标的关系，他们在之后的反向传播的公式推导中会很有用

这里考虑用均值平方误差即 MSE 作为损失函数 $J$，$sigmoid$ 函数作为激活函数，当然这两个换成别的函数的话推导过程也是类似的

$$ J = \frac{1}{2k}\sum_{j=1}^k(a_j^L-y_j)^2 $$

反向传播的直觉理解

我发现，在深入了解细节之前，从高层次的角度理解一个概念总是能带来帮助。我们知道，深度学习模型的训练过程就是要让模型的预测 $a^L_j$ 越接近真实值 $y_j$ 越好。那么 $a^L_j$ 跟什么有关呢？根据样本的真实值 $y_j$，可以计算 $a^L_j$ 和 $y_j$ 的误差，计算出误差之后，我们肯定知道要增大还是减小 $a^L_j$ 才能让模型的预测更好。而我们能够改变的量只有：第 $L - 1$ 层和第 $L$ 层之间的每个权重 $w^L_{jk}$，偏置项 $b_j^L$，或者是第 $L-1$ 层的激活函数的输出值 $a^{L-1}_k$，但是 $a_k^{L-1}$ 并无法直接改变，它是由更前面的权重和偏置项的值决定的。当我们从后往前根据预测的误差，考虑要如何修改每一层的权重和偏置项的时候，就是在做反向传播¹。

上述过程解释了 $a_j^L$ 想要如何调整模型的权重和偏置项。当然，我们还需要考虑输出层中除了$a_j^L$ 以外的神经元的“意见”。他们各自对如何改变模型的权重和偏置项的“意见”并不一定相同。最后，我们需要考虑输出层中所有神经元的意见来更新模型的权重和偏差

反向传播的四个公式

反向传播的核心就是下面四个公式

公式一

$$ \delta_j^L=\frac{\partial J}{\partial a_j^L}\sigma’(z_j^L) $$

其中 $L$ 为模型的层数，在我们前面定义的模型中 $L=3$，$\delta_j^L$ 表示第 $L$ 层即输出层的第 $j$ 个神经元的梯度信息

顺带一提，用矩阵和向量的角度可以把上面的公式改写为$\delta^L=\nabla J\odot \sigma’(z^L)$。其中 $\odot$ 表示按元素（element-wise）乘

📒 公式一计算的是输出层的每个神经元的梯度

推导过程⬇️ $$ \begin{aligned} \delta_j^L&=\frac{\partial J}{\partial z_j^L} \\\ &=\sum_k\frac{\partial J}{\partial a_k^L}\frac{\partial a_k^L}{\partial z_j^L} \\\ &=\frac{\partial J}{\partial a_j^L}\frac{\partial a_j^L}{\partial z_j^L}\ (only\ \frac{\partial a_j^L}{\partial z_j^L}\ne 0) \\\ &=\frac{\partial J}{\partial a_j^L}\frac{\partial \sigma(z_j^L)}{\partial z_j^L}\ \\\ &=\frac{\partial J}{\partial a_j^L}\sigma’(z_j^L) \end{aligned} $$

公式二

$$ \delta^l=((w^{l+1})^T\delta^{l+1})\odot \sigma’(z^l) $$

📒 公式二计算的是任意层 $l$ 的梯度向量，注意这个公式如何将第 $l$ 层的梯度向量和第 $l+1$ 的梯度向量联系起来。它让我们可以用后面的层的梯度向量计算前面的层的梯度向量

推导过程⬇️ $$ \begin{aligned} \delta_j^l&=\frac{\partial J}{\partial z_j^l} \\\ &=\sum_k\frac{\partial J}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^l} \\\ &=\sum_k\delta_k^{l+1}\frac{\partial }{\partial z_j^l}z_k^{l+1} \end{aligned} $$

注意其中 $\frac{\partial }{\partial z_j^l}z_k^{l+1} = \frac{\partial }{\partial z_j^l}\ \sum_pw^{l+1}_{kp}\sigma(z_p^l)+b^{l+1}_k$

只有当 $p=j$ 的时候才可导，因此上面公式的解是 $w^{l+1}_{kj}\sigma’(z_j^l)$

即，我们证明了$\delta_j^l=\sum_k\delta_k^{l+1}\ w^{l+1}_{kj}\sigma’(z_j^l)$

$\sum_k\delta_k^{l+1}w^{l+1}_{kj}$ 其实就是计算 2 个向量的内积，因此可以将其改写为向量形式 - $\delta^l=((w^{l+1})^T\delta^{l+1})\odot \sigma’(z^l)$

公式三

$$ \frac{\partial J}{\partial b^l_j}=\delta_j^l $$

📒 公式三可以用来计算模型中任意一个偏置项（Bias）的梯度

推导过程⬇️ $$ \begin{aligned} \frac{\partial J}{\partial b^l_j}&= \frac{\partial J}{\partial z^l_j}\frac{\partial z^l_j}{\partial b^l_j} \\\ &= \delta_j^l \frac{\partial}{\partial b^l_j}\sum_kw^l_{jk}a^{l-1}_j+b^l_j\\\ &= \delta_j^l \end{aligned} $$

注意上面的第一个等号和公式一的推导类似，我直接跳过了去掉 $\sum_k$ 的过程

公式四

$$ \frac{\partial J}{\partial w_{jk}^l}=a_k^{l-1}\delta_j^l $$

📒 公式四可以用来计算模型中任意一个权重（Weight）的梯度

推导过程⬇️ $$ \begin{aligned} \frac{\partial J}{\partial w_{jk}^l}&=\frac{\partial J}{\partial z^l_j}\frac{\partial z^l_j}{\partial w_{jk}^l} \\\ &=\frac{\partial J}{\partial z^l_j}\frac{\partial }{\partial w_{jk}^l}\sum_pw_{jp}^la_p^{l-1}+b_j^l \\\ &=\delta_j^l\frac{\partial }{\partial w_{jk}^l}\sum_kw_{jk}^la_k^{l-1}+b_j^l \\\ &=\delta_j^la_k^{l-1} \end{aligned} $$

反向传播算法

基于前面讨论的公式，可以知道反向传播算法的工作流程

1. 前向传播，计算每个 $z_j^l$，$a_j^l$
2. 根据公式一计算输出层的梯度向量 $\delta^L$
3. 从后往前
   1. 根据公式二计算每一层的梯度向量 $\delta^l$，注意我们总是可以根据 $\delta^{l+1}$ 计算出 $\delta^l$
   2. 根据公式三可以计算出每个偏置项 $b^l_j$ 的梯度，它等于 $\delta^l_j$
   3. 根据公式四可以计算出每个权重 $w^l_{jk}$ 的梯度，它等于 $\delta_j^la_k^{l-1}$

上面这个过程也回答了——为什么反向传播是一个高效的算法这个问题

• 👍 根据公式二，计算第 $l$ 层的梯度向量 $\delta^l$ 的时候 $\delta^{l+1}$ 已经算好了，不用从头从输出层开始推导
• 👍 根据公式三和公式四，直接算出了损失函数对当前层权重和偏置项的梯度，而不是其他什么中间的梯度结果

总结

上面就是反向传播算法的整个流程，公式和记号还是颇多的～但还是比较好理解的，在复习反向传播算法的时候发现了一些可能帮助读者理解反向传播的点：

• 反向传播是针对单个样本的算法，所以推导的时候考虑一个样本作为模型的输入就行了
• 推导公式的时候从某个神经元的角度思考，然后归纳为向量形式。而不是一上来就从向量形式入手，当然实力好的当我没说

收工，感谢阅读👋

参考