如何记忆红黑树的操作
引言
如果你点进了这一篇文章,相信你也跟我一样:红黑树学一次忘一次,又要做树的旋转,又要给节点重新上色,导致每次都是学完了就忘记。我也曾经仔细阅读过 CLRS 写的《算法导论》,但是上面的分类讨论只是让我更加头疼
当然,记住一项东西的最佳方式永远都是理解它,而最近看到斯坦福的 CS166 高级数据结构课程的课件的时候,我似乎理解了红黑树————红黑树和 2-3-4 树是等同(isometry)的数据结构,他们只是用了不同的方式表示 2-3-4 树1,这意味着我们可以通过 2-3-4 树上的节点变化,进而推导出红黑树上的形状和颜色的变化,而 2-3-4 树的节点变化,是简单很多的
在开始之前,我假定你对以下的内容很熟悉
- 你知道 2-3-4 树或者说 B 树是什么,2-3-4 树其实就是 B 树的一种。你需要知道在 2-3-4 树上的删除和插入操作如何进行,什么时候会发生节点的 overflow、underflow,以及这种时候要如何处理
- 你知道如何在二叉搜索树中插入和删除节点,毕竟红黑树本身就是保证高度是 $O(log\ n)$ 的二叉搜索树,要知道如何找到插入位置,如何确定要删除的节点等
- 你需要知道红黑树和 2-3-4 树的定义,需要理解红黑树有什么性质,以及在红黑树上插入节点、删除节点都可能打破哪些性质
最重要的,你不需要记住红黑树的旋转和颜色变化操作,因为只要你掌握了今天要讲的技巧,你就可以在红黑树的操作和 2-3-4 树上的操作之间建立直觉上的联系
节点映射定义
2-3-4 树上一共只有可能有下面 3 种节点:
- 2-node,有 2 个孩子,含 1 个 key
- 3-node,有 3 个孩子,含 2 个 key
- 4-node,有 4 个孩子,含 3 个 key
通过节点映射关系,我们可以将 2-3-4 树上的节点转化为对应的红黑树结构,反之依然。注意他们都是黑色节点开始,后面我们会多次用到这个映射表
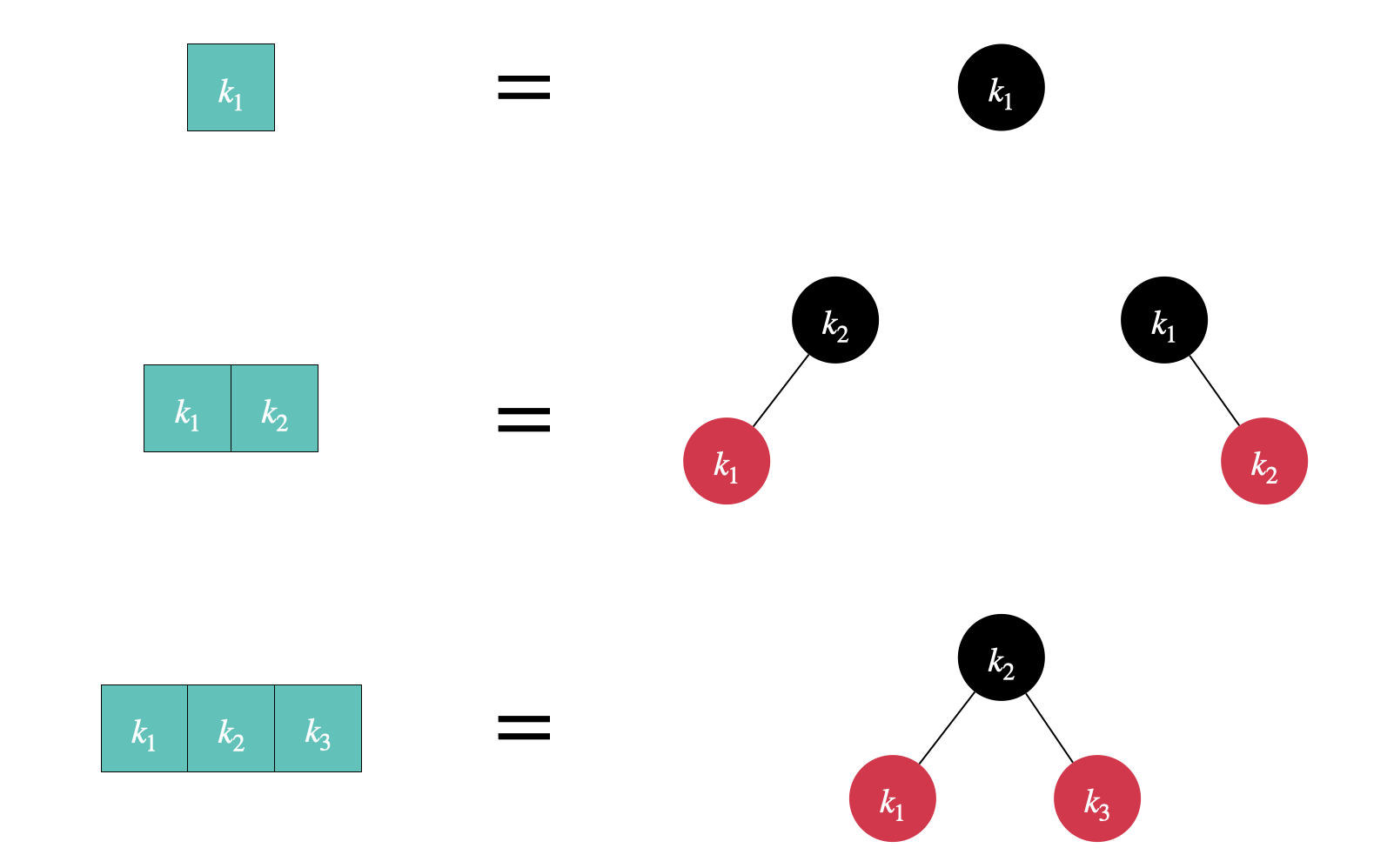
左边是 2-3-4 树的 2-node, 3-node, 4-node,右边是对应的红黑树结构
新增节点操作
先来简单回顾一下,往红黑树节点中新增一个节点的步骤
- 红黑树是二叉搜索树,所以一开始按照二叉搜索树插入节点的办法找到要插入的位置
- 如果新插入的点会成为根节点(即本来的红黑树为空),则新插入的节点为黑色;其他情况则为红色,因为红黑树有个性质是从任一节点到其每个叶子节点的路径都包含相同数量的的黑色节点,让新插入的节点的颜色为红色就可以维护这个性质。下面我们只考虑新插入的节点为红色的情况
新插入的节点是红色的话这意味着可能打破红黑树的另外一个性质——不能有 2 个连续的红色节点。红黑树中通过树旋转和节点重新上色🎨解决了这个问题,但是规则比较复杂不好记
在讲解具体例子之前,先概括一下通用的思路:
- 找到要插入的位置插入新节点,设置新节点的颜色为红色
- 将红黑树上「违背规则的部分」转化为「2-3-4 树上等同的形式」
- 思考如果在 2-3-4 树的这个等价形式要如何处理
- 在 2-3-4 树上处理好之后,再转化为红黑树,此时形状和颜色都决定好了
💡 为了帮助读者理解如何在 2-3-4 树和红黑树之间变换,在变换前后的等同部分,我用了一个带颜色的透明框标记了
💡 我选择了直接用具体的数值而不是抽象的符号,因为这样会更加直观,更方便读者在 2-3-4 树和红黑树之间找到联系
新增节点的父节点是黑色节点
一个简单情况是,新插入的红色节点的父节点是黑色,此时满足要求仍然是红黑树,不需要任何改动

新增节点的父节点是红色节点而且不存在 uncle 节点
接下来,让我们考虑稍微复杂点的情况,新增节点的父节点是红色节点,红黑树不允许这样的情况出现。此时它可能有也可能没有 unlce 节点,让我们先考虑它没有 uncle 节点的情况,可以很轻松画出下面几种可能的形式
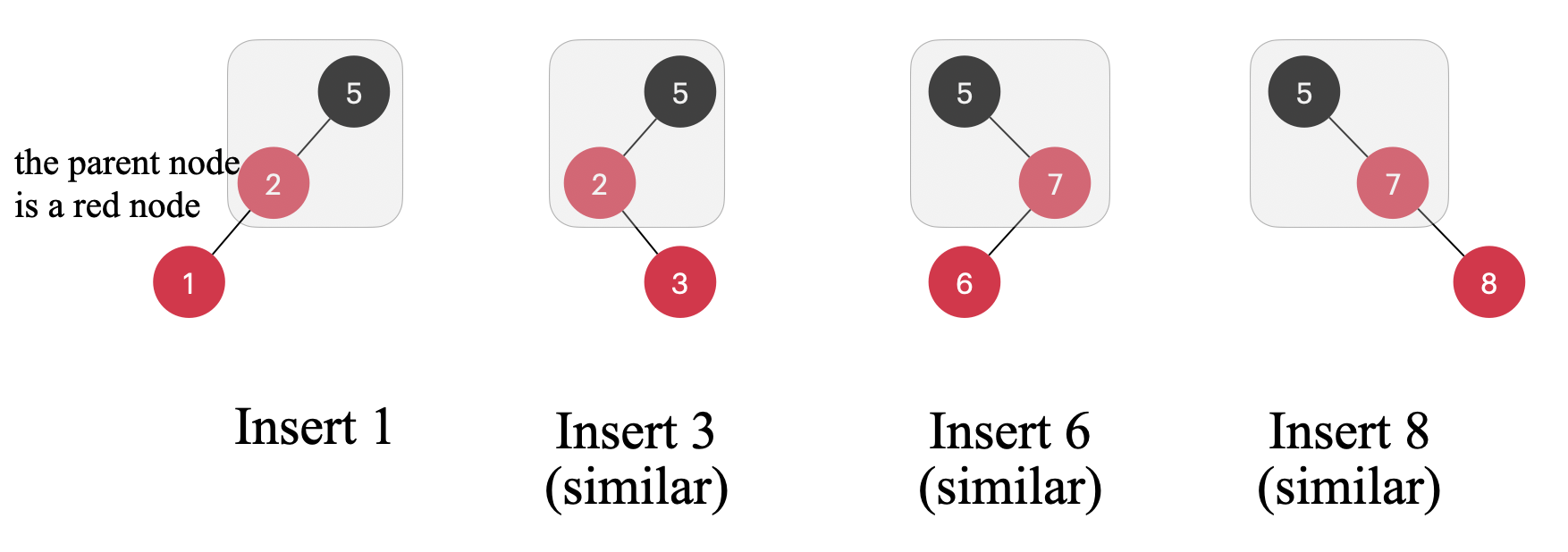
注意这几种都是等价的,下面我只展示上图第一个例子是如何操作的
💡 后面当我们讨论其他情况的时候,他们也可能会存在等价形式,但其实方法都大同小异,我会每次挑其中一个讲
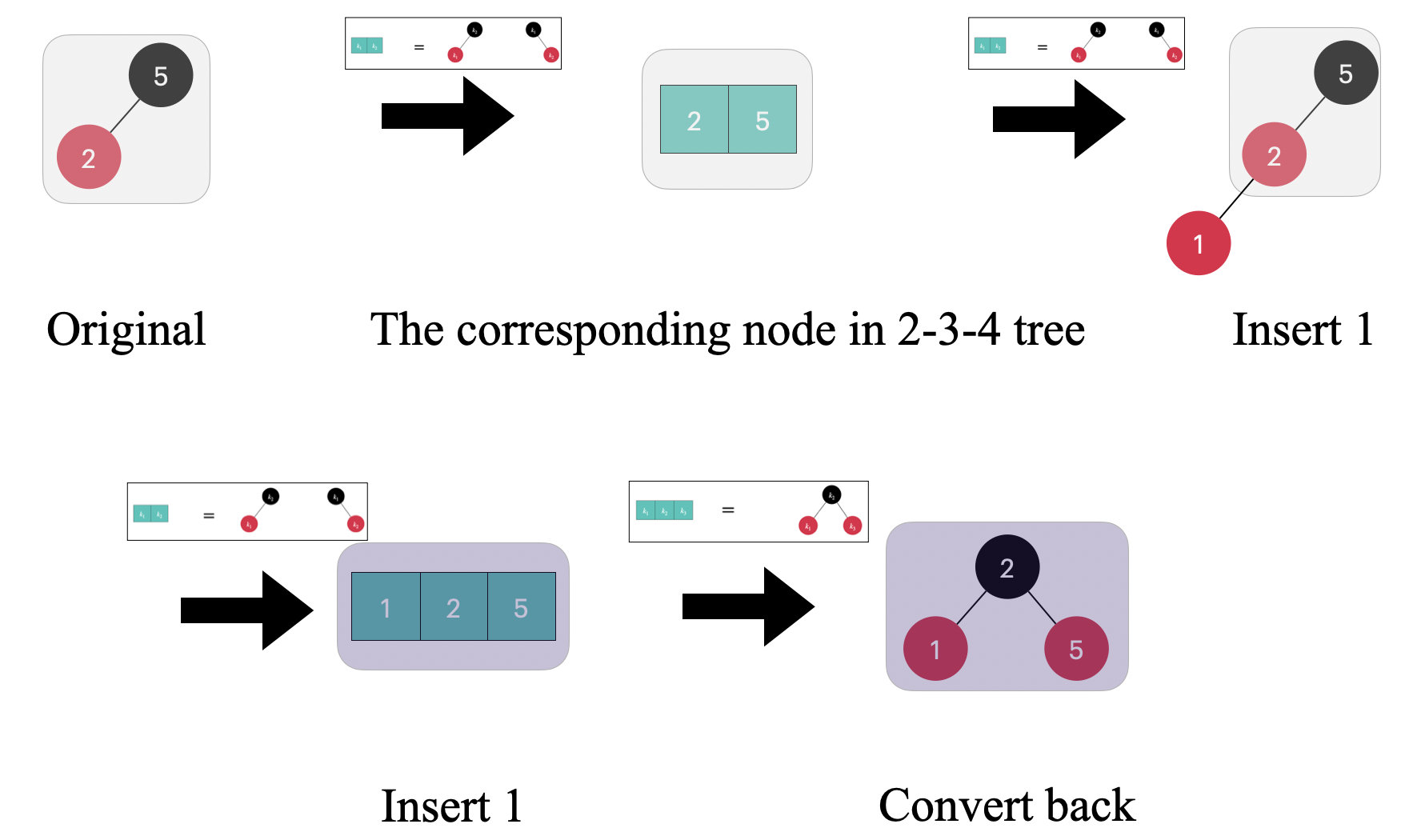
根据之前提到的节点映射关系,插入前的红黑树正好对应 2-3-4 树上的 3-node,然后我们在红黑树中插入节点 1,与此同时,我们在 3-node 上也进行插入操作,得到了一个 4-node,4-node 符合 2-3-4 树要求,所以也不需要分裂节点,此时再根据节点映射关系转化为红黑树
此时你可能觉得似乎 2-3-4 树没有带来多大方便,因为这里一个简单右旋,然后重新染色并不是一件复杂的事情,但是之后随着情况越来越复杂,你会发现 2-3-4 树的理解角度容易理解很多🤔️
新增节点的父节点是红色节点而且存在 uncle 节点
现在让我们来考虑它有 uncle 节点的情况,它可能为黑色,也可能为红色
先来看看如果 uncle 节点为黑色的其中一种可能情况
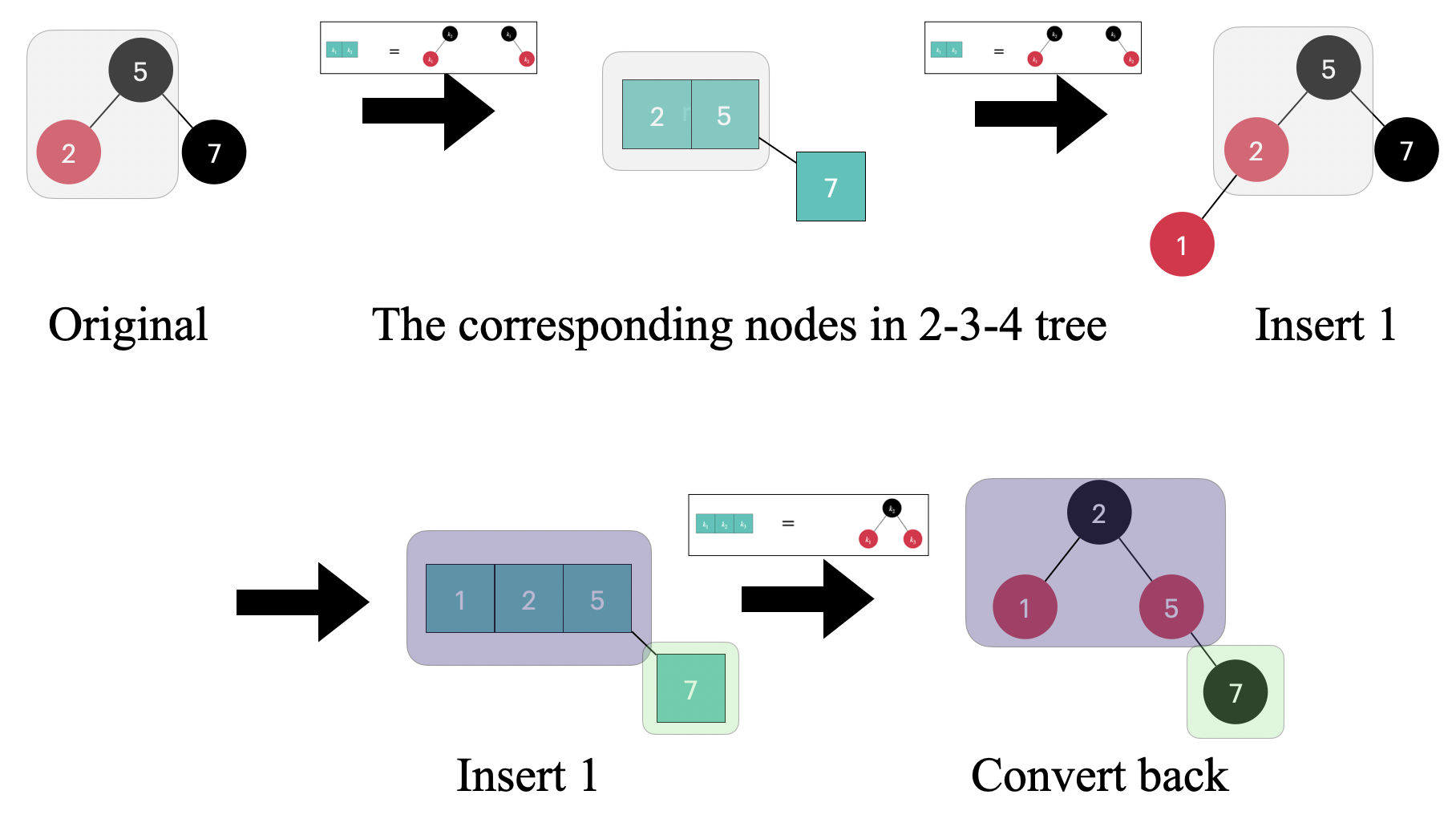
根据节点的映射关系,我们可以把红黑树的 2, 5 映射为 2-3-4 树上的 3-node,而红黑树上的 7 就映射为一个 2-node,在红黑树上插入 1,因此也在 2, 5 这个 3-node 上插入 1,得到的 1, 2, 5 根据节点映射关系,映射为一个黑色节点加两个红色孩子节点,而 7 则映射为一个黑色节点
那如果 uncle 节点是红色呢?比如像下面这样
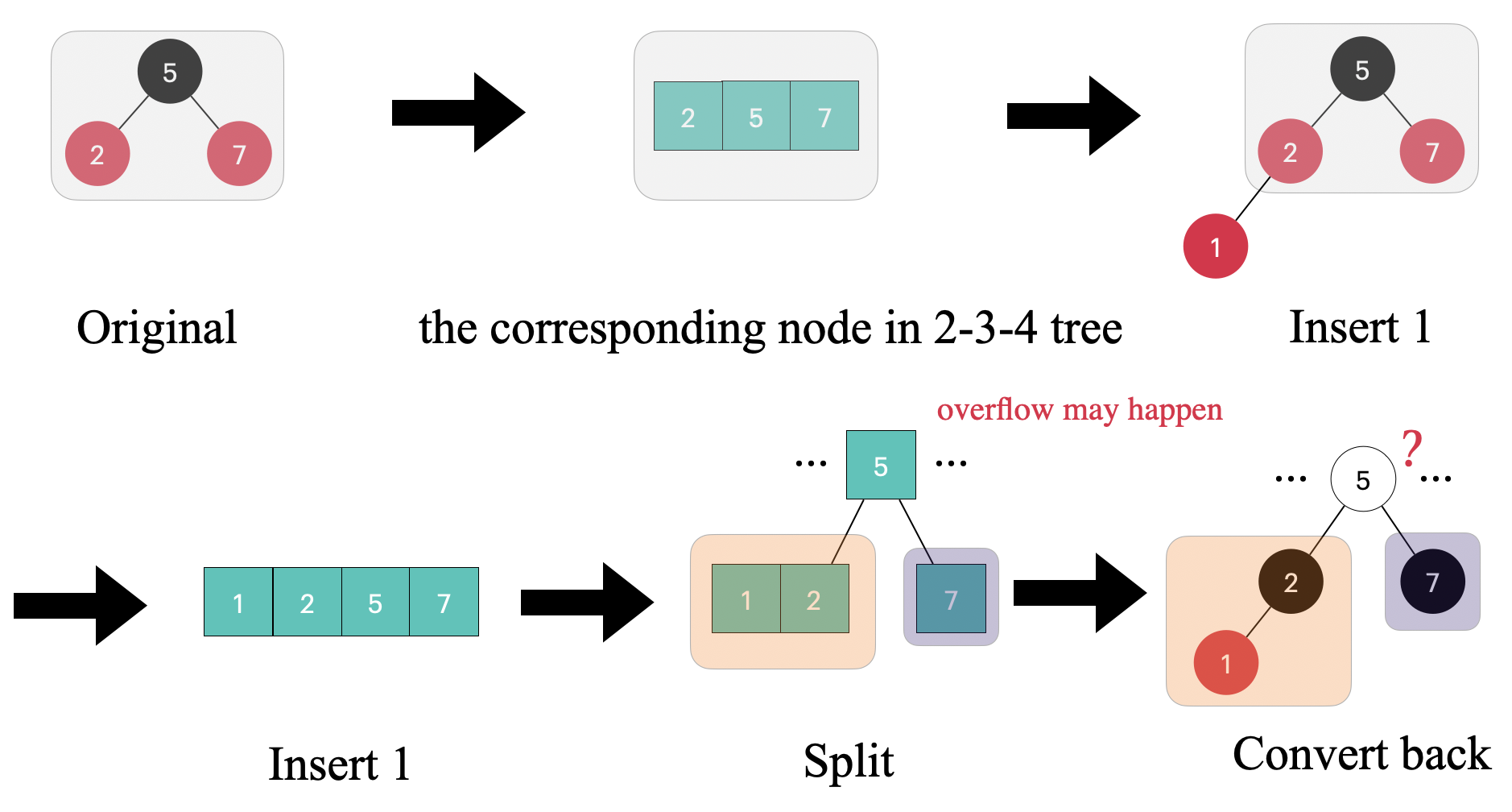
这个会稍微复杂一些,因为在等价的 2-3-4 树插入 1 之后我们需要对 1, 2, 5, 7 进行分裂操作,也就是将图上的节点 5 插入到父节点中,因为不知道父节点什么情况,因此节点 5 两边用省略号表示,在 2-3-4 树中往父节点插入一个节点意味着可能导致父节点也 overflow,最坏的情况我们是需要这样一路一直修改回去
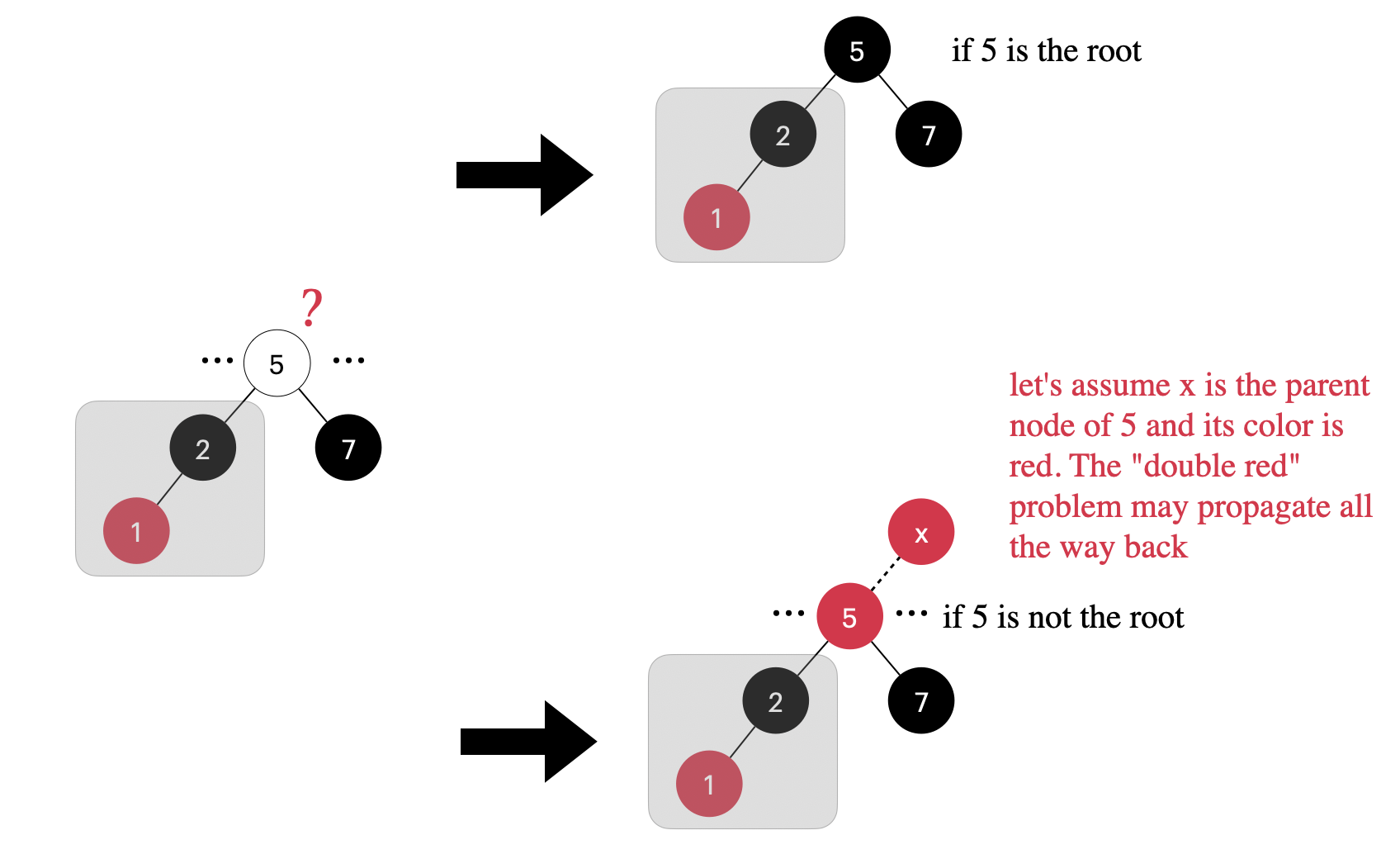
另外注意一个问题,这里插入的新节点的祖先(grandparent)节点应该是红色节点,例子中的节点 5 就是新增节点 1 的祖先节点。这样才能保证从任一节点到其每个叶子节点的路径都包含相同数量的的黑色节点,但是有个例外,那就是祖先节点是红黑树的根节点的时候,那么它就应该是黑色,下图清晰展示了这 2 种可能
删除节点操作
先来简单回顾一下,在红黑树节点中删除一个节点的步骤
- 按照二叉搜索树删除节点的方式,找到要删除的节点,假设要被删除的节点是
z - 那么根据
z的节点颜色可以分出下面两种情况z是红色节点,删除红色节点是比较容易的,因为不会打破红黑树的性质,就是正常的二叉搜索树删除节点的操作,这里不展开z是黑色节点,删除黑色节点可能打破红黑树的性质——从任一节点到其每个叶子节点的路径都包含相同数量的的黑色节点,在红黑树中,遇到这种情况仍然是需要用树的旋转和节点重新上色🎨解决问题。下面的讨论主要考虑的是这种情况
被删除的节点有红色右孩子
💡 注意,根据二叉搜索树的删除节点操作,我们知道要删除的节点
z一定没有左孩子,如果它有右孩子的话,我们记为y
💡 黄色节点表示不知道颜色或者是不关心它什么颜色
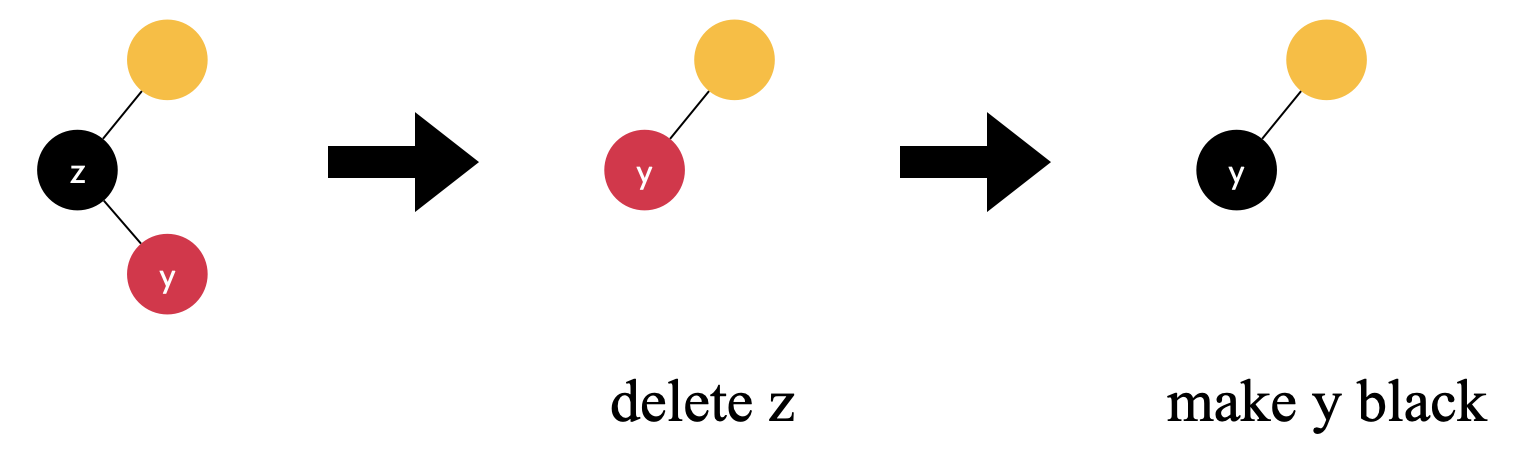
删除黑色的 z,然后用它的红色右孩子 y 代替 z
被删除的节点有黑色右孩子
我们暂时用黑色的 y 代替被删除的黑色的 z,并且记 y 为 “double black” 节点,在图上,黑色节点 + 圆环就表示 “double black”2
💡 “double black” 对于红黑树而言,意味着我们要让这边有 2 个黑色节点;对于 2-3-4 树而言,那就对应 2-3-4 树中删除 2-node 的 key之后引发的 underflow
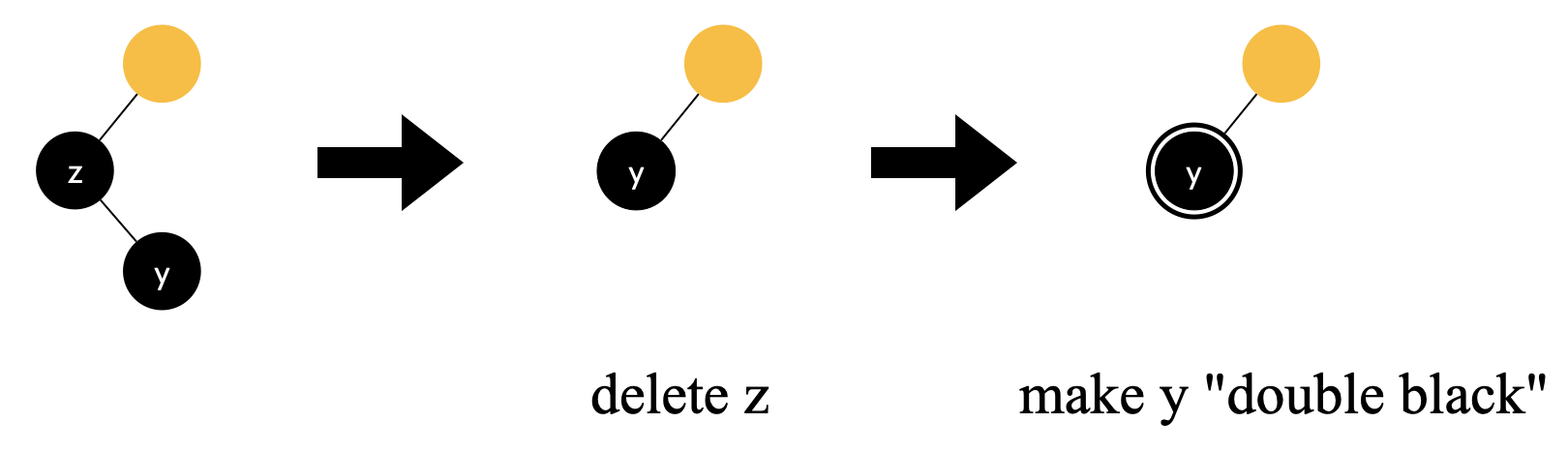
删除黑色的 z,然后用它的黑色右孩子 y 代替 z,标记 y 为 “double black” 节点
接下来我们要根据「“double black” 的兄弟节点」来分情况推导
如果兄弟节点是黑色而且有「一个红色孩子」
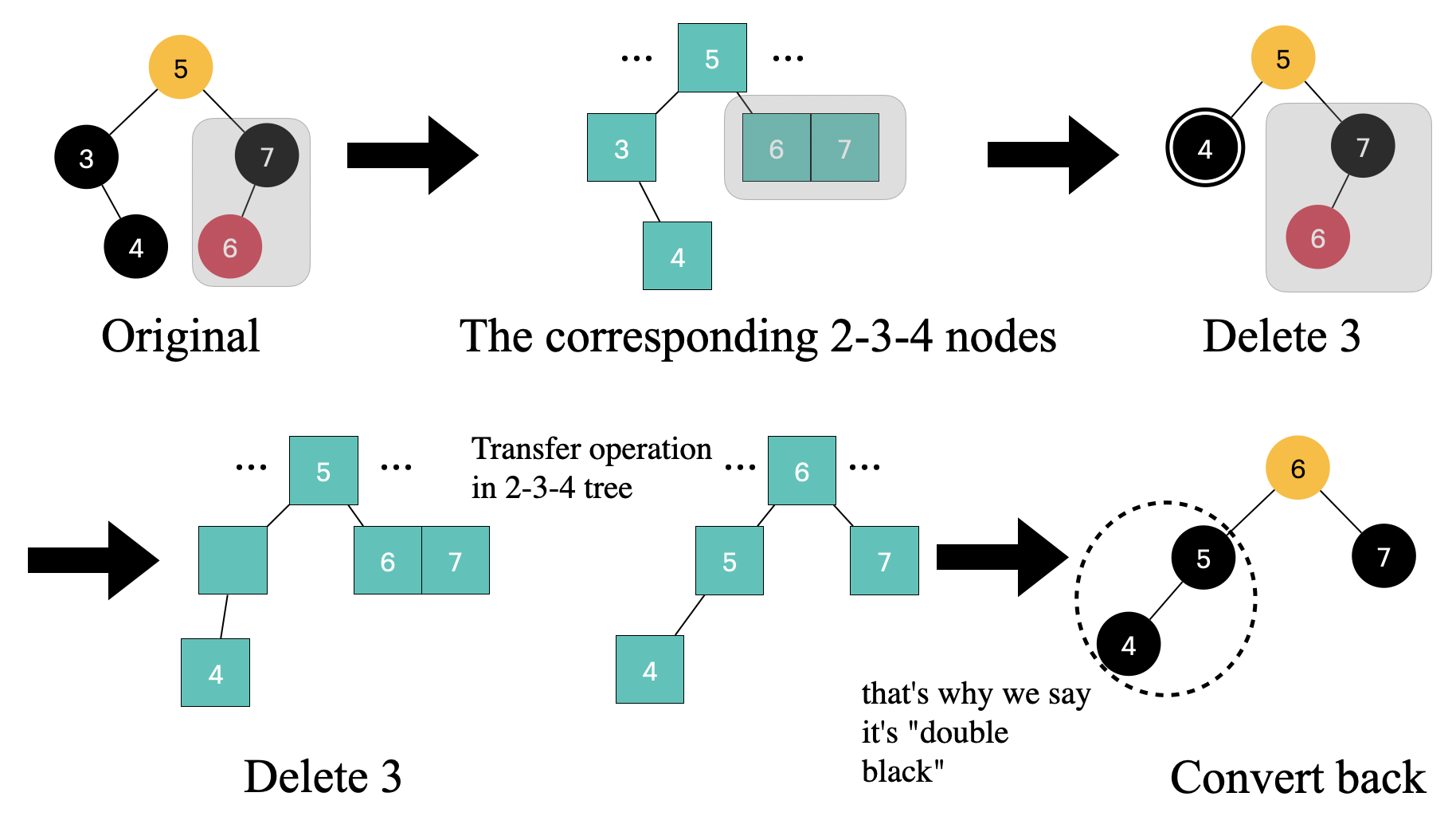
在上面的例子,转化为等价的 2-3-4 树上的删除节点操作,在 2-3-4 树中遇到这种情况需要执行 transfer 操作,因为兄弟节点 6, 7 是一个 3-node,还有得借。transfer 操作也就是父节点的 key 移动到被删除的节点的位置,然后兄弟节点的最小的 key 移动到父节点填补空缺
💡 注意看,现在
4和5是 2 个黑色节点,先前这里是一个特殊的 “double black” 节点,现在有 2 个黑色节点了,“double black” 也就没有必要了。这也是它叫做这个名字的原因,我们需要提醒自己这里需要 2 个黑色节点
💡 注意这里节点
6的颜色就是本来节点5的颜色
如果兄弟节点是黑色而且有「两个黑色孩子」
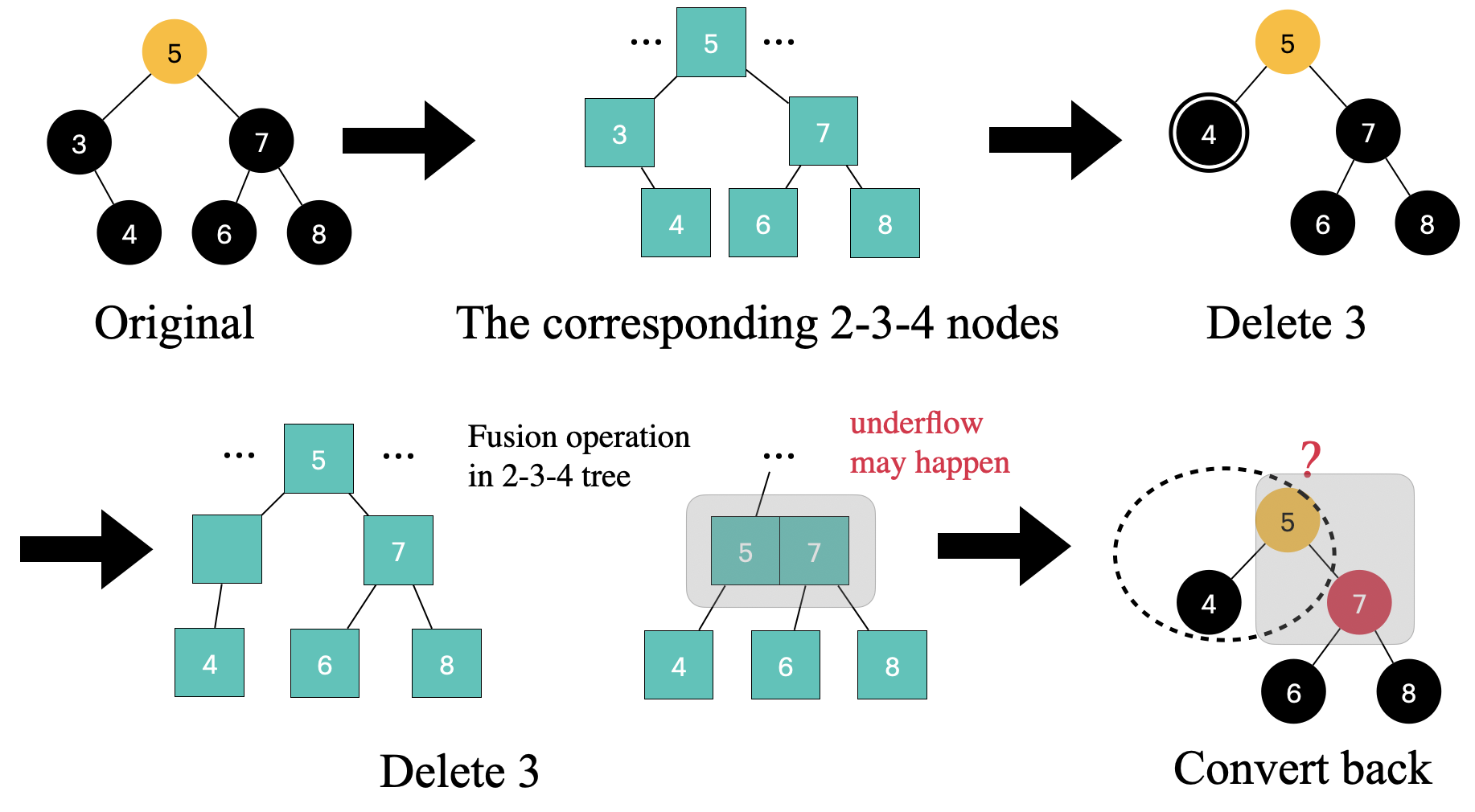
在上面的例子,转化为等价的 2-3-4 树上的删除节点操作,在 2-3-4 树中遇到这种情况需要执行 fusion 操作,因为兄弟节点 7 是一个 2-node,没得借。fusion 操作就是从父节点那边借一个 key 下来,然后和兄弟节点合并,成为一个 3-node,也就是图上的 5, 7
💡 但是注意这里的 Fusion 操作找父节点借了一个 key,这可能导致父节点 underflow 了,正如前面我们在新增节点的时候可能 overflow
理论上来说,这个例子的节点 5 应该是黑色(根据前面对节点映射的规定),这样才能满足 “double black” 的要求,但是不要忘了 5 自己是有颜色的
- 如果
5本来是红色,那么把5变成黑色是没有问题的,因为现在的节点7就是红色,红黑树还是平衡的 - 如果
5本来是黑色,那么把5变成黑色是有问题的,因为还是会少了一个黑色节点,那么节点5就变成了新的 “double black” 节点,我们还得向上继续调整。这恰恰是对应了 2-3-4 树中发生了 underflow 的情况,那么我们就要 bototm-up 一路调整回去。最后如果发现根节点是一个 “double black” 节点,那么把根节点变成黑色节点即可
如果兄弟节点是红色而且有「两个黑色孩子」
最后一种情况,如果兄弟节点为红色,而且有 2 个黑色孩子
💡 注意,如果兄弟节点是红色,他们的共同父节点肯定是黑色,因为红黑树不允许有 2 个连续的红色节点
这个可以通过取巧的办法来转化为前面情况:
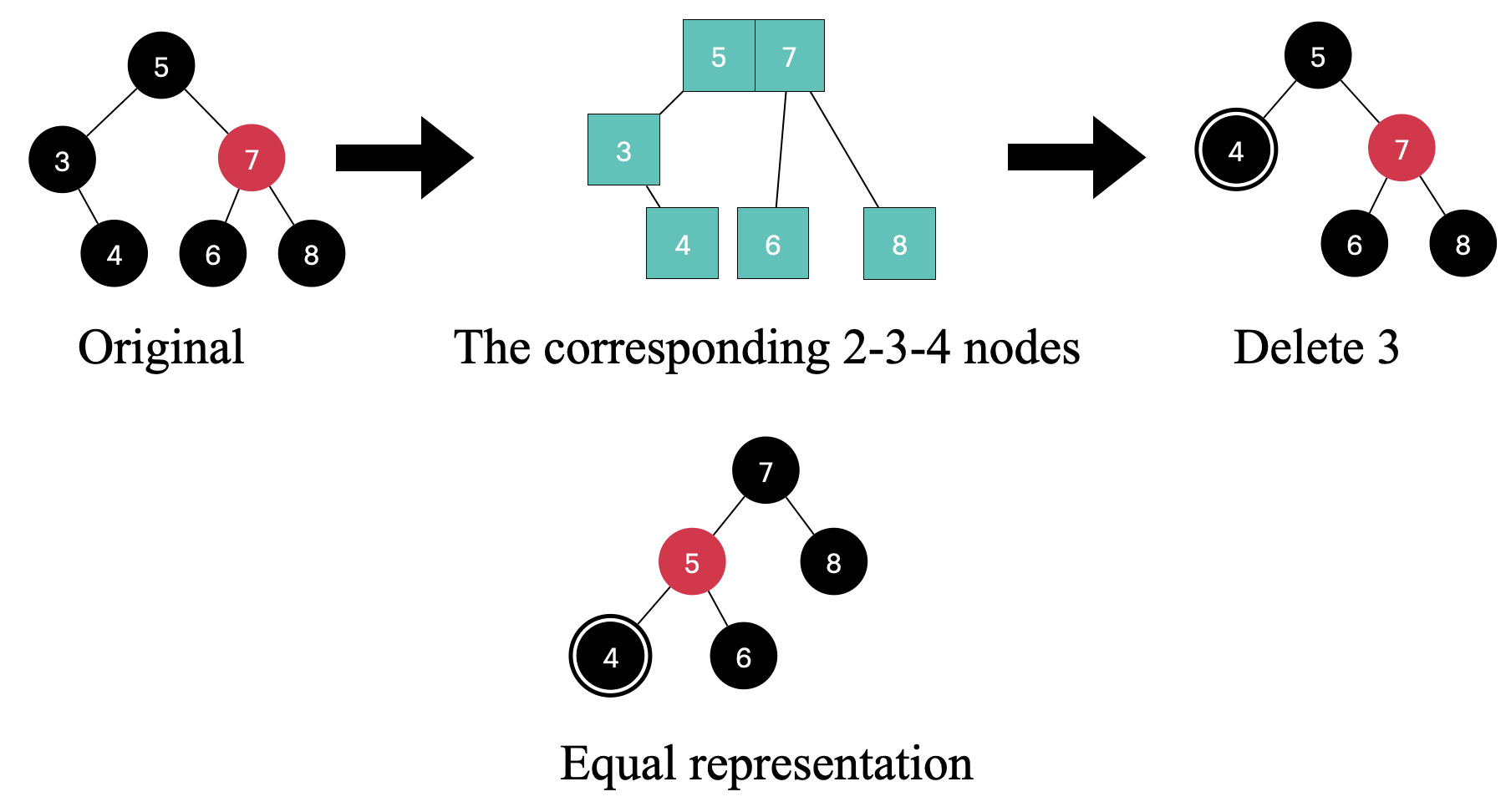
现在节点 4 的兄弟节点就是黑色节点了,转化为前面的情况,可以按照前面的办法处理
总结
经过前面的例子展示,我们发现可以在 2-3-4 树上思考要如何处理,处理完成之后转变回红黑树,而 2-3-4 树的节点插入和删除操作都是比较简单的,这也是这套方法的价值所在,最重要的是,终于可以不用记住旋转顺序和怎么交换颜色了👏
推荐阅读
关于 2-3-4 树和红黑树的对应关系,还有下面的几个参考资源可以阅读
- CS166. Balanced Trees, Part I
- CS166. Balanced Trees, Part II
- CS280. Mapping 2-3-4 trees into Red-Black trees