Pytorch 张量的 strides 格式是什么
引言
尽管我已经使用 Numpy 和 Pytorch 好长一段时间了,但我一直不知道他们是如何实现底层的张量(tensor),而且这么高效。最近在看 Deep Learning Systems 这门课,终于有机会尝试自己实现张量,实现一遍之后对张量的理解更深刻了🧐
作为 Pytorch 的使用者有必要理解底层的张量存储原理吗?我觉得是有必要的,大多数情况下理解底层原理都能让你更好理解上层的东西,比如理解张量的存储原理之后有助于你会回答下面这几个问题
- 广播操作涉及到数组的拷贝吗?
- Pytorch 的
contiguous中是干什么的?为什么需要这个函数?
按行存储与按列存储
让我们从简单的二维数组出发,二维数组在内存中占据连续的位置,但是要按行存储还是按列存储这点可能不相同
比如现在有下面这个 $2\times 3$ 的二维数组 A
[[0.2949, 0.9608, 0.0965],
[0.5463, 0.4176, 0.8146]]如果是按行存储,那么内存中的排列(这里记为 A_in_row)是:
[0.2949, 0.9608, 0.0965, 0.5463, 0.4176, 0.8146]按行存储的时候,要访问 (i, j) 位置的值的公式是
A[i][j] = A_in_row[i * A.shape[1] + j]如果是按列存储,那么内存中的排列(这里记为 A_in_col)是:
[0.2949, 0.5463, 0.9608, 0.4176, 0.0965, 0.8146]按列存储的时候,要访问 (i, j) 位置的值的公式是
A[i][j] = A_in_col[j * A.shape[0] + i]Strides 格式
张量在底层可以是按行存储也可以是按列存储。Numpy 和 Pytorch 都采用了按行存储的方式,任何维度的张量在底层存储都占据着内存中连续的空间,那么问题来了,我们如何访问到我们想要的位置的数据?
答案就是 strides 格式。strides 格式可以看成是前面两种索引格式的泛化版本,假设现在有一个 $N$ 维的张量 A(假设维度从 0 开始),它的底层存储为 A_internal,我们想要访问 A[i0][i1][i2]...,那么索引的方式如下:
A[i0][i1][i2]... = A_internal[
stride_offset
+ i0 * A.strides[0]
+ i1 * A.strides[1]
+ i2 * A.strides[2]
+ ...
+ in-1 * A.strides[n-1]
]Strides 格式有两个组成部分
offset- 表示张量相对于底层存储A_internal的偏移量strides数组,长度和张量的维度一样,strides[i]表示张量在第 $i$ 个维度上移动“一个单位”需要在内存上跳过多少个元素
举例来说,前面提到的二维数组的例子,如果用 strides 的格式来理解的话,应该是下面这样
A[i][j] = A_in_row[
0
+ i * A.shape[1]
+ j * 1
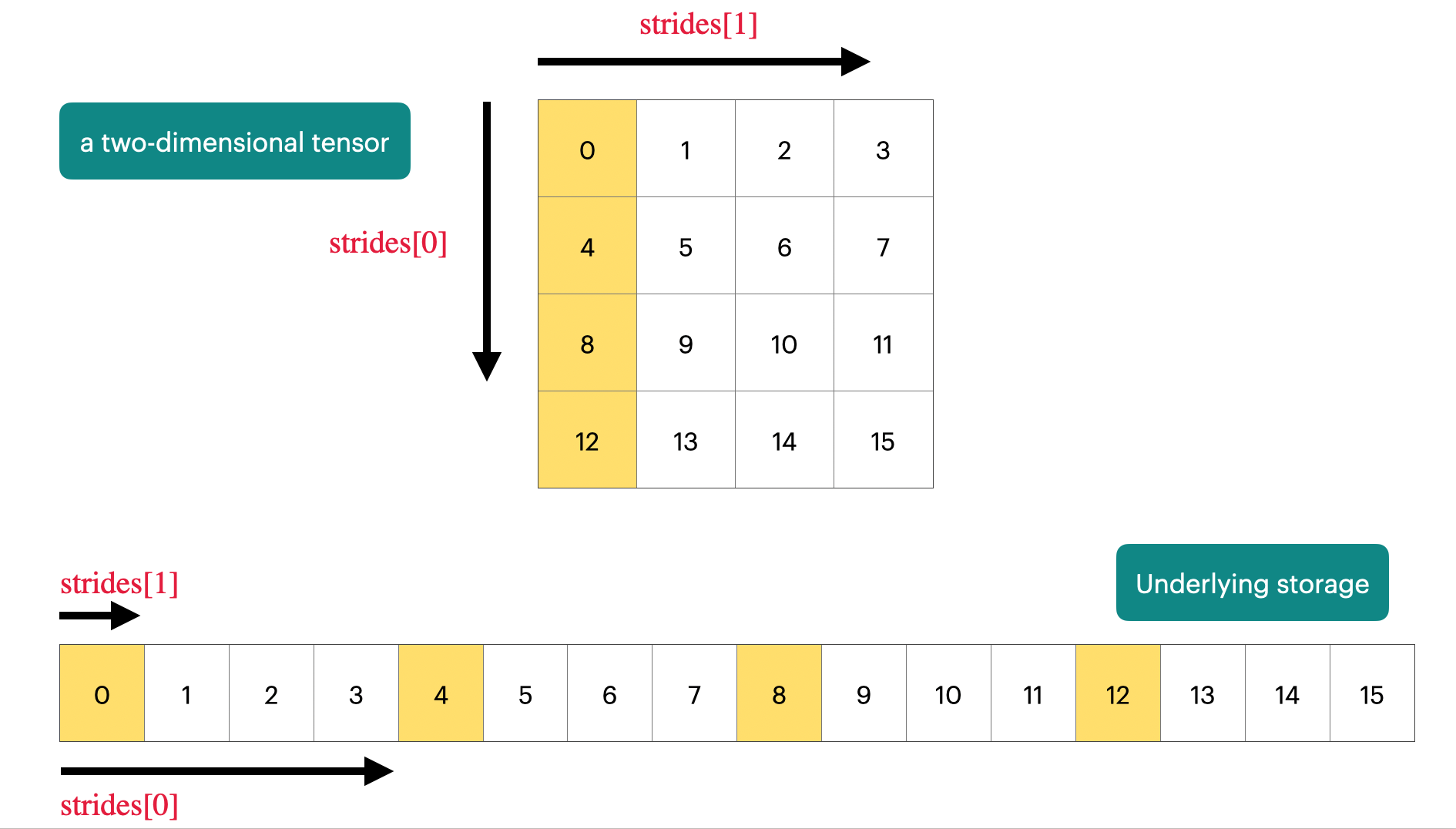
]即对于一个大小为 (A.shape[0], A.shape[1]) 的二维数组,它的 offset 是 0,strides = [A.shape[1], 1](row-major)。🤔️ 也就是说,每次在第一个维度上要跳跃“一个单位”,需要跳过底层的 A.shape[1] 个元素,A.shape[1] 也就是行的长度
我做了下面这张图片,希望能够帮助你理解 :)
🧐 那么如何得到 $N$ 维张量的 strides 数组?假设要求解的是 strides[k] 即第 $k$ 个维度的 stride,我们知道它的语义是「在第 $k$ 维上移动“一个单位”需要在内存上跳过多少个元素」,如果这个张量的底层存储在内存上是连续存储(紧凑格式),那就是 「$k+1,k+2,…,N-1$ 维度的大小的乘积」,如果 $k=N-1$,那么 strides[N - 1] = 1
数学公式就是下面这样, $$strides[k]=\prod_{i=k+1}^{N-1}shape[i]$$
💡 再次强调,上面的公式只有在张量的底层存储在内存上是连续存储(紧凑格式)的时候成立
Why strides?
知道了 strides 的存储格式之后,我们还要理解为什么这么设计,strides 究竟给我们带来了什么?最大的好处是:很多关于张量的操作都可以是零拷贝(Zero-copy)的。通过 strides 格式,「底层存储」和「视图」之间是分离开的,下面我来讲解一下几个常见的操作
print_internal 函数
在开始之前,让我们先写一个函数获取 Pytorch 的张量底层存储
首先是 Pytorch 提供的 data_ptr() 这个方法,他会返回张量底层存储表示的第一个元素的内存地址
然后通过 Pytorch 提供的 storage().nbytes() 就可以知道张量的底层存储在内存上占据了多大的空间1,而张量的 dtype 属性则告诉了我们每个元素占据多大,比如 torch.float32 就是 4 个字节
最后通过 ctypes.string_at(address, size=-1) 函数就可以读取这个张量为 C 的字符串(buffer),而 torch.frombuffer 可以从一个 buffer 创建出 tensor
通过上面几个步骤,我们就可以还原出 Pytorch 底层的数组表示,下面命名为 print_internal 函数
def print_internal(t: torch.Tensor):
print(
torch.frombuffer(
ctypes.string_at(t.data_ptr(), t.storage().nbytes()), dtype=t.dtype
)
)然后我们创建一个维度为 (1, 2, 3, 4) 的张量 t 并观察它的底层表示,后面的操作讲解会基于这个张量 t
torch.arange(0, 24).reshape(1, 2, 3, 4)
print(t)
# tensor([[[[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]],
# [[12, 13, 14, 15],
# [16, 17, 18, 19],
# [20, 21, 22, 23]]]])
print(t.stride())
# (24, 12, 4, 1)
print_internal(t)
# tensor([0, 1, 2, 3,
# 4, 5, 6, 7,
# 8, 9, 10, 11,
# 12, 13, 14, 15,
# 16, 17, 18, 19,
# 20, 21, 22, 23])按照我们前面说的从张量的维度推导 stride 的方法,我们不难知道这个 tensor 的 stride 应该是 (2 * 3 * 4, 3 * 4, 4, 1) 也就是 (24, 12, 4, 1)
在 Pytorch 里面,我们可以通过调用 tensor 的 stride() 方法获得 stride,可以看到,确实跟我们手动计算出来的一样🤔️
permute 操作
假设我们用 permute 重新排列了各个维度,那么 strides 如何变化?
print(t.stride())
# (24, 12, 4, 1)
print(t.permute((1, 2, 3, 0)).is_contiguous())
# True
print(t.permute((1, 2, 3, 0)).stride())
# (12, 4, 1, 24)
print(t.permute((0, 2, 3, 1)).is_contiguous())
# False
print(t.permute((0, 2, 3, 1)).stride())
# (24, 4, 1, 12)
print(t.permute((1, 0, 3, 2)).is_contiguous())
# False
print(t.permute((1, 0, 3, 2)).stride())
# (12, 24, 1, 4)
print_internal(t.permute((1, 2, 3, 0)))
# tensor([0, 1, 2, 3,
# 4, 5, 6, 7,
# 8, 9, 10, 11,
# 12, 13, 14, 15,
# 16, 17, 18, 19,
# 20, 21, 22, 23])从上面的例子我们可以看出来,permute 操作不会影响 offset,但通常情况下,permute 操作会导致底层存储不紧凑。我们可以通过 permute 之后的新的维度 new_shape 然后根据定义计算出 strides,但是更快的办法是,直接在 strides 上也做一样的 permute 操作即可。print_internal 函数的输出证明了 permute 操作是 Lazy 的2
broadcast_to 操作
广播操作是比较有意思的,在不了解张量的存储原理之前,你可能以为广播操作就是在对应的维度上拷贝多份,但其实,根本就没有发生拷贝,只是修改了 strides 数组的值而已。更确切来说,Pytorch 会把被广播的维度(本来的维度大小是 1)的 stride 设置为 03
比如现在我们在第一个维度上做广播,观察广播之后的维度大小,以及 strides 数组的变化情况
print(t.broadcast_to((2, 2, 3, 4)).is_contiguous())
# False
print(t.broadcast_to((2, 2, 3, 4)).shape)
# torch.Size([2, 2, 3, 4])
print(t.stride())
# (24, 12, 4, 1)
print(t.broadcast_to((2, 2, 3, 4)).stride())
# (0, 12, 4, 1)
print_internal(t.broadcast_to((2, 2, 3, 4)))
# tensor([0, 1, 2, 3,
# 4, 5, 6, 7,
# 8, 9, 10, 11,
# 12, 13, 14, 15,
# 16, 17, 18, 19,
# 20, 21, 22, 23])你(可能)会惊讶地发现,Pytorch 确实没有在广播的时候拷贝对应维度的张量,仅仅只是修改 strides 数组了而已。回忆 strides[i] 的含义,被广播的维度的 stride 设置为 0 意味着这个维度上移动“一个单位“并不需要在内存上跳过元素,也就是在被广播的维度上我们一直在访问的是同一块区域
reshape 操作和 contiguous 操作
索引操作可能会修改 offset,因为索引之后形成的张量不一定从本来底层存储的第一个元素开始,同时索引操作可能会索引到底层存储中的「非连续」部分。因此我们可以通过索引操作来研究 reshape 操作和 contiguous 操作是如何起作用的
现在假设我们想要从 t 拿到下面这个张量
[[[2,
6,
10],
[14,
18,
22]]]对应的索引操作如下
print(t[:, :, :, 2])
# tensor([[[ 2, 6, 10],
# [14, 18, 22]]])注意到这个操作同时符合我前面说的:
offset改变了,因为现在是从2而不是从0开始了- 索引到的元素在本来的内存上不是连续的
下面的代码验证了我们的猜想
print(t.storage_offset())
# 0
print(t[:, :, :, 2].storage_offset())
# 2
print(t[:, :, :, 2].is_contiguous())
# False现在来观察底层存储
print_internal(t[:, :, :, 2])
# tensor([ 2, 3,
# 4, 5, 6, 7,
# 8, 9, 10, 11,
# 12, 13, 14, 15,
# 16, 17, 18, 19,
# 20, 21, 22, 23
# 1152921504606846976, -8070441752123218147]])
# ignore the last row because t.data_ptr() has changed but t.storage().nbytes()
# kept the same.
# As a result, we read 2 invalid elements and get 2 meaningless valuesPytorch 的张量有个方法叫做 storage_offset 可以拿到张量相对于底层存储的偏移量,可以看到现在从底层存储的第二个位置开始了,第二个位置恰好是 t[:, :, :, 2] 的第一个元素 2。而打印出底层存储你会发现,底层存储还是本来的数组
注意这里有个小问题,因为底层存储没有变化,
t.storage().nbytes()跟原来一样。但是data_ptr()会给我们第二个元素的地址,导致最后print_internal打印底层存储的时候会多打印 2 个无效的位置(也就是上面的最后一行),所以得到了 2 个没有意义的数字
🤔️ 这个时候我们尝试执行 reshape(3, 2) 并观察底层存储情况
print_internal(t[:, :, :, 2].reshape(3, 2))
# tensor([ 2, 3,
# 4, 5, 6, 7,
# 8, 9, 10, 11,
# 12, 13, 14, 15,
# 16, 17, 18, 19,
# 20, 21, 22, 23
# 1152921504606846976, -8070441752123218147]])reshape 操作之后发现底层存储还是没有变化,这恰好对应文档里面所说的:可能的情况下,reshape 之后,返回的张量尽可能是同一份存储4
但如果我们想要 reshape 之后的张量在底层的存储是紧凑的呢?此时就可以紧跟着调用 contiguous 方法
print_internal(t[:, :, :, 2].reshape(3, 2).contiguous())
# tensor([ 2, 6, 10, 14, 18, 22])😺 可以发现,contiguous 之后确实底层存储就紧凑了,此时的 strides 数组应该符合我们前面提到的公式:
# before contiguous
print(t[:, :, :, 2].reshape(3, 2).stride())
# (8, 4)
# after contiguous
print(t[:, :, :, 2].reshape(3, 2).contiguous().shape)
# (3, 2)
print(t[:, :, :, 2].reshape(3, 2).contiguous().stride())
# (2, 1)🧐 一个比较有挑战性的问题,索引操作会如何影响 strides?
让我们以刚才的索引操作为例子,首先,索引之后得到新的维度应该是 (1, 2, 3),显然 [:, :, :, 2] 这样的索引导致底层存储在内存上不紧凑,因此规律不适用,那么只能从定义上出发,假设 t[:, :, :, 2] 的 strides 是 [x, y, z]
先观察 t[:, :, :, 2] 包含哪一些元素
print(t[:, :, :, 2])
# tensor([[[ 2, 6, 10],
# [14, 18, 22]]])因为我定义的张量是从 0 开始的整数,因此我们可以直接观察值的变化来计算 strides 的变化(这是一个小技巧)
- 对于
z,从2 -> 6 -> 10,每次跳过了 4 个位置,所以z = 4 - 对于
y,2 -> 14,6 -> 18,10 -> 22,每次都跳过了 12 个位置,因此y = 12 - 对于
x,因为底层存储并没有改变,原本的张量t的stride[0] = 24,如果张量t的第一个维度不是 1 而是一个更大的值,我们还是每次会跳过stride[0]个元素,所以x = 24
所以 t[:, :, :, 2] 的 strides 应该是 (24, 12, 4)
让我们来调用一下 API 看这是否正确
print(t.stride())
# (24, 12, 4, 1)
print(t[:, :, :, 2].stride())
# (24, 12, 4)
# what if the first dimension is not 1 but 2?
another_t = torch.arange(0, 48).reshape(2, 2, 3, 4)
print(another_t[:, :, :, 2])
# tensor([[[ 2, 6, 10],
# [14, 18, 22]],
# [[26, 30, 34],
# [38, 42, 46]]])
# you can see that 2 -> 26, 6 -> 30, 10 -> 35
# , so the stride[0] = 24 is true上面的代码验证了我们的猜想
但是,索引操作可能远远比我们这里讲解的 [:, :, :, 2] 复杂得多,比如 [2, 1:3, 1:6:3] 这种,此时 strides 和 offset 又该如何变化?这里不展开,但是可以放一个提示:把每个格式都变成 Python 的 Slice 对象,然后从 strides[i] 的定义出发进行推导
总结
可以看到,Pytorch 的张量的不少操作都是通过改变 strides 的 offset 或(和)strides 数组实现的,这让很多操作维持了零拷贝开销,因此效率会很高,而且,这使得我们可以把不少张量操作实现为 Lazy 的。理解 strides 格式有助于构建张量的 mental model,它能够让你更好理解张量的操作的代码。顺便推荐一下这个视频,在这个视频中,可以看到如何操纵 strides 来实现高效的卷积操作
现在我们可以回答前面我抛出的问题了:
- 广播操作涉及到数组的拷贝吗?
- 并没有拷贝,只是修改了
strides数组
- 并没有拷贝,只是修改了
- Pytorch 的
contiguous中是干什么的?为什么需要这个函数?- 因为
contiguous之后,张量的底层存储是内存紧凑的,虽然有拷贝的开销,但是后续执行一些张量相关的操作的时候内存局部性会更好
- 因为