论文阅读: Outrageously Large Neural Networks-The Sparsely-Gated Mixture-of-Experts Layer

Motivations

模型能力跟模型参数量有关系，模型参数量越多，数据越多，效果就越好。但训练成本也成倍上升。为了解决这个问题，大家提出了很多种条件计算（Conditional Computations）的方案，顾名思义，某些条件满足的情况下才会计算，这样就可以不增加训练成本的同时增加模型参数量，提升模型效果

作者提出了 Sparsely-Gated Mixture-of-Experts Layer (MoE) 架构，如下所示¹

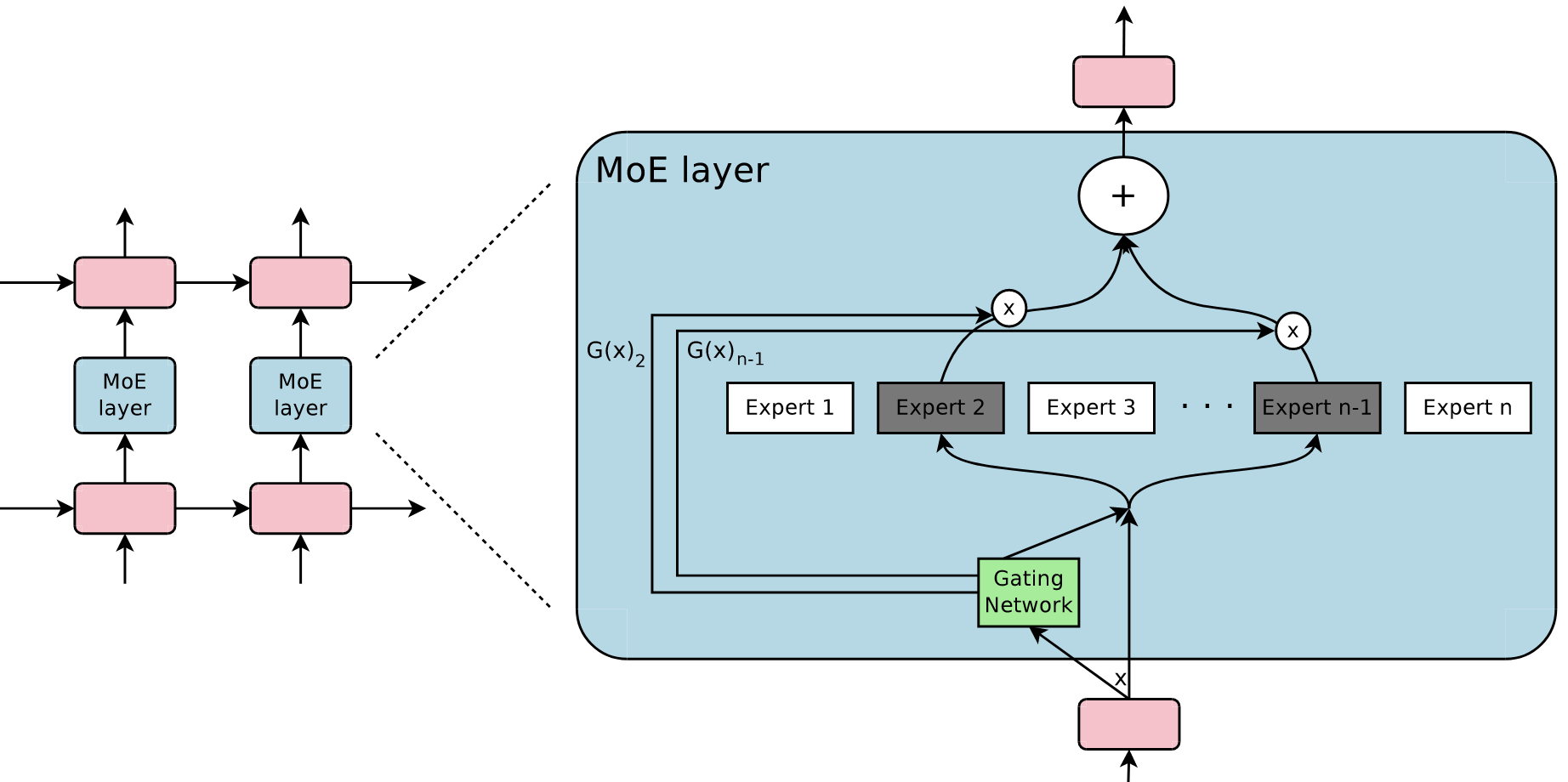
MoE 架构

MoE 层包含 $n$ 个专家（Expert） $E_1, E_2, …, E_n$，以及一个门控网络 $G$，门控网络 $G$ 的输出是一个长度为 $n$ 的向量

用 $x$ 表示输入，$G(x)$ 表示门控网络的输出，$E_i(x)$ 表示专家 $E_i$ 的输出，那么 MoE 的输出 $y$ 可以表示为

$$ y=\sum_{i=1}^nG(x)_iE_i(x) $$

注意这里的 $G(x)_i$ 的下角标 $i$ 表示 $G(x)$ 的第 $i$ 个位置。所以上面的式子告诉我们 MoE 的输出就是对 $n$ 个专家的输出的加权和

可想而知，如果 $G(x)_i =0$，那么对应的 $E_i(x)$ 就没有必要计算，训练成本就这么降低了。如果 $G(x)$ 的很多位置都 $=0$，即门控网络 $G$ 的输出是稀疏的，那么训练成本可以减少非常多

Expert

所谓的专家就是神经网络，论文里面用的是简单的 FFN 层

Gating Network

一个简单的 idea 是将输入 $x$ 乘以一个权重矩阵 $W_g$，然后用 $\texttt{Softmax}$ 函数（注意 $\texttt{Softmax}$ 的输出和为 1）

$$ \texttt{Softmax}(x\cdot W_g) $$

注意，它不是稀疏的。所以作者用了如下的手段让它是稀疏的

1. 得到 $x\cdot W_g$ 之后叠加一个可以调节的高斯噪声
2. 保留其中值最大的 TopK 个，剩下的设置为 $-\infty$（注意 $-\infty$ 在经过 $\texttt{Softmax}$ 就得到了 0）
3. 最后再用 $\texttt{softmax}$

这里解释一下什么叫做可以调节的高斯噪声，作者将 Softplus 函数乘以高斯噪声，同时控制 Softplus 的输入为 $x\cdot W_{noise}$，这里的权重矩阵 $W_{noise}$ 也起到了调节的作用。这样每一个不同的 MoE 层的噪声可以单独控制

将上面的文字表述翻译为公式就是

$$ \begin{split} G(x)&=\texttt{Softmax}(KeepTopK(H(x), k)) \\\ H(x)_i&=(x\cdot W_g)_i + \texttt{StandardNormal}()\cdot\texttt{Softplus}\big((x\cdot W_{noise})_i\big) \\\ KeepTopK(v,k)_i&= \begin{cases} v_i & \texttt{if }v_i\texttt{ is in the top }k\texttt{ elements of } v\\\ -\infty & \texttt{otherwise} \end{cases} \end{split} $$

MoE 优化

Batch size

Batch Size 开大一点效率才会高，采用 MoE 架构之后，假设 Batch Size 是 $b$，每一次都会从 $n$ 个专家中选择 $k$ 个激活，那么对于每一个专家来说，等价的 Batch Size 是

$$ \frac{kb}{n} $$

可想而知，大 Batch Size 就应该调大 $b$，但要是显存放不下呢？针对这个问题，作者提出了如下的建议——采用数据并行，但每个专家只有 1 份，在多个设备上共享，其他层（包括门控网络）都是每个设备 1 份。注意，每个专家都只会收到跟自己有关的样本来进行计算和更新，假设有 $d$ 个设备，每个设备处理 $b$ 个样本，那么这样优化之后每个专家等价的 Batch Size 是

$$ \frac{kbd}{n} $$

这意味着，可以通过增加设备来调大 Batch Size

充分利用所有专家

作者在实验中发现，MoE 架构的门控网络 $G$ 几乎总是会选择少数几个专家，而且随着训练的进行这个情况会不断恶化，因为被更新的专家越有概率被选中

为了缓和这个问题，作者增加了一个约束——定义专家的重要性 $Importance$。现在假设有 1 个 Batch 的数据（用 $X$ 表示）进来，对于专家 $E_i$，它的重要性 = $\sum_{x\in X} G(x)_i$，因此所有专家的重要性 $Importance(X)$ 可以表示为

$$ Importance(X)=\sum_{x\in X}G(x) $$

注意 $Importance(X)$ 是一个长度为 $n$ 的向量，每个位置是对应专家的重要性得分。根据 $Importance(X)$ 可以定义一个额外的损失

$$ L_{importance}(X)=w_{importance}\cdot\texttt{CV}(Importance(X))^2 $$

这个损失会被加到总的损失里。其中 $w_{importance}$ 是超参数，$\texttt{CV}$ 表示变异系数（Coefficient of Variation），衡量了离散程度。不同专家彼此的得分越不相同，离散程度越大，损失则越大。因此，增加这个损失函数鼓励不同专家有一样的重要性

实验结果

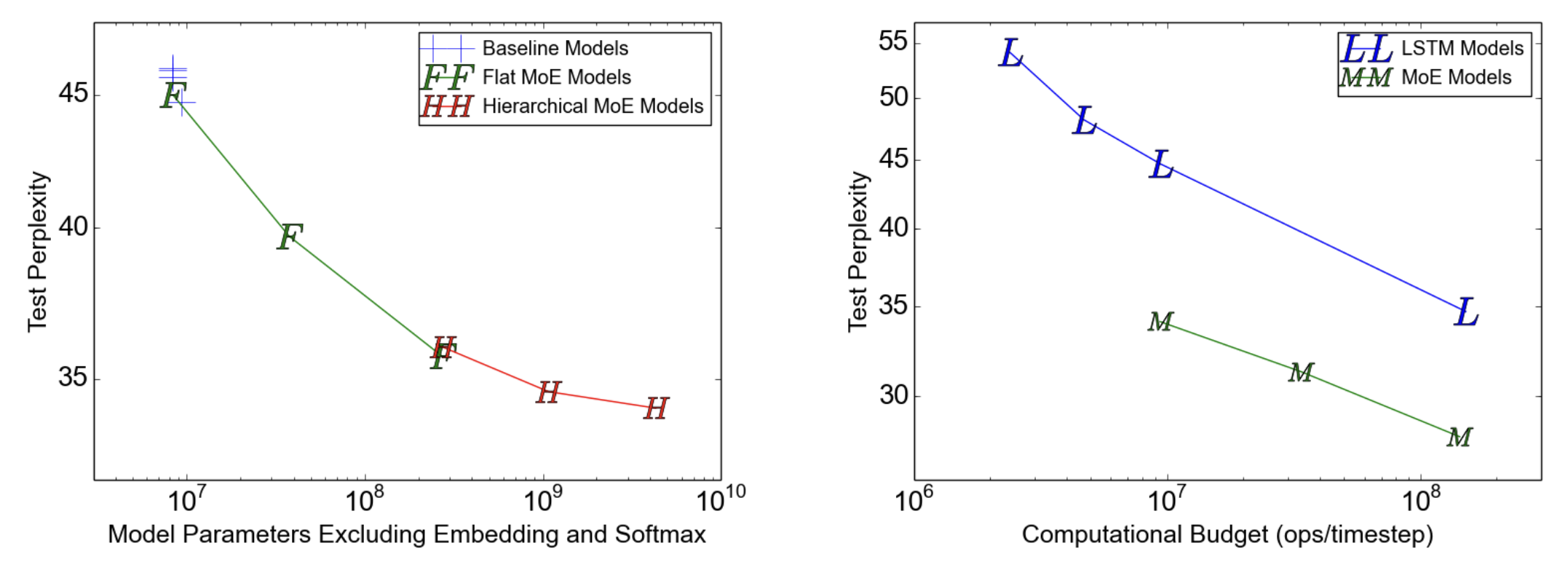
上面的图¹说明了下面几个结论

1. 不管是单层 MoE 还是多层 MoE，都比 Baseline 好
2. 多层 MoE 效果比单层 MoE 稍微好些
3. 相同训练成本下（纵轴），采用 MoE 架构的模型表现更好

总结

可以看到，MoE 架构允许我们在增加模型参数量的同时，训练成本不会成比例上升。并且在模型推理的时候，每次只有 K 个专家在处理，因此推理也更快了。不过，整个模型还是要都加载到显存里面，不能只加载几个专家🤔

Refs