KNN 算法是什么

什么是 KNN

KNN 允许我们根据一堆已知类别的样本判断一个新的样本 $\mathbf x$ 的类别，判断的原理是综合考虑距离它最近的 $K$ 个样本的类别

那么可想而知，有这么几个核心的问题值得研究

• $K$ 应该是多少？
• 如何度量“距离”？
• 如何综合最近的 $K$ 个样本的类别的结果？

关于 K 的选取

$K$ 越大，参考的样本就越多，理论上会越准确，但实际上考虑太多的样本会把距离不近的样本也包括进来

$K$ 太小的话，又会导致 KNN 的预测的方差比较大

所以，$K$ 不能太大也不能太小，那么在实际上操作的时候：可以让 $K$ 从小到大变化，观察验证集上的表现。用 $K$ 作为横轴，验证集上的表现作为纵轴画出曲线，这个曲线的拐点就是最佳的 $K$，这就是所谓的“肘部法则”

也可以考虑用交叉验证法选择最佳的 $K$

关于距离

假设每一个样本都用长度为 $d$ 的向量表示，那么样本之间的距离计算可以考虑用欧几里得距离

$$ \texttt{distance}(\mathbf x,\mathbf y)=\sqrt{\sum_{i=1}^d(x_i-y_i)^2} $$

如何综合 K 个最近邻居的结果

在找到新样本的 $K$ 个最近的邻居之后，让这 $K$ 个邻居进行投票，投票数最多的类别就是新样本的类别

算法实现

Scikit-Learn 库提供了 API 用于创建 KNN 分类器，在开始之前，我们先生成一个数据集用于演示

import numpy as np
np.random.seed(40)
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(
    n_samples=100,
    n_features=2,
    n_informative=2,
    n_redundant=0,
    n_clusters_per_class=1,
    random_state=40,
)
X_train, X_temp, y_train, y_temp = train_test_split(
    X, y, test_size=0.2, random_state=40
)

X_valid, X_test, y_valid, y_test = train_test_split(
    X_temp, y_temp, test_size=0.5, random_state=40
)

为了对数据集有更好的了解，这里可以画一个散点图。结果如下所示

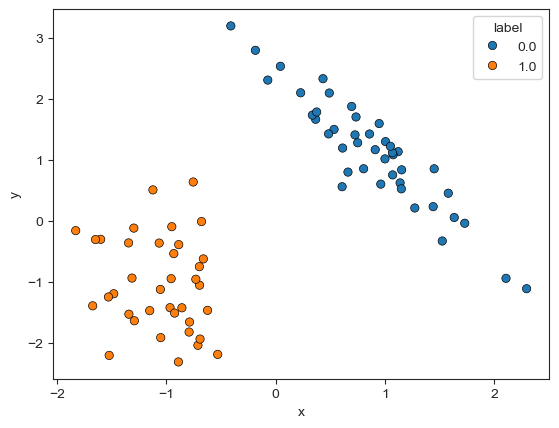
接下来创建一个 KNN 分类器，在训练集 X_train 上“训练”一个 KNN 模型

from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=5)
neigh.fit(X_train, y_train)

现在假设有一个新的样本 [0, 0]，就可以用这个模型判断它的类别

test_point = [0, 0]
neigh.predict([test_point])
# array([1])

同样的，可以画出散点图看一下，其中的黑色 $\times$ 表示邻居，红色的 $\times$ 是用于测试的样本 [0, 0]

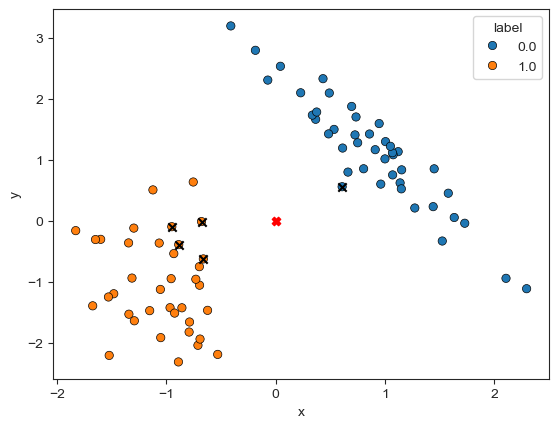
根据结果来看，4 个邻居是类别 1，1 个邻居是类别 0，所以 [0, 0] 的类别是 1

FAQ

不平衡数据集可以用 KNN 吗

不推荐，因为样本不平衡会导致用 KNN 算法得到的分类几乎总是样本多的类别

K 的大小和模型复杂度的关系

一个有趣的问题是：$K$ 越大 KNN 越复杂？还是 $K$ 越小？答案：$K$ 越小模型越复杂，也因此更容易“过拟合”

这句话可以反过来理解，$K$ 最大的情况下等于所有样本的个数 $N$，此时只要是新样本，会总是被判断为 $N$ 个样本中最多的类别，这样的模型显然太简单了

KNN 应该做 Normalize 吗？

显然是的，不然计算距离的时候，数值比较大的特征对距离的影响更大

KNN 可以用于回归问题吗？

可以，比如取 $K$ 个邻居的平均值，但一般 KNN 还是用来做分类问题

KNN 可以如何改进？

朴素的 KNN 采用投票法，即每一个邻居节点的贡献度是一样的，一个改进方向是：修改每一个邻居节点的贡献度，比如越近的邻居贡献度越大。一个常用的权重是 $1/d$，这里的 $d$ 是到邻居到新样本的距离