论文阅读: Generalization through Memorization: Nearest Neighbor Language Models
目录
Motivation
语言模型解决 2 种问题
- 用一个特征向量表示句子前缀
- 使用该特征向量预测下一个 token
本文提出的 $k\texttt{NN-LM}$ 基于这么一个假设:学习特征向量表示比预测下一个 token,因此本文的方法主要基于该假设进行设计
kNN-LM
下面这张图概括了 $k\texttt{NN-LM}$ 的思想1
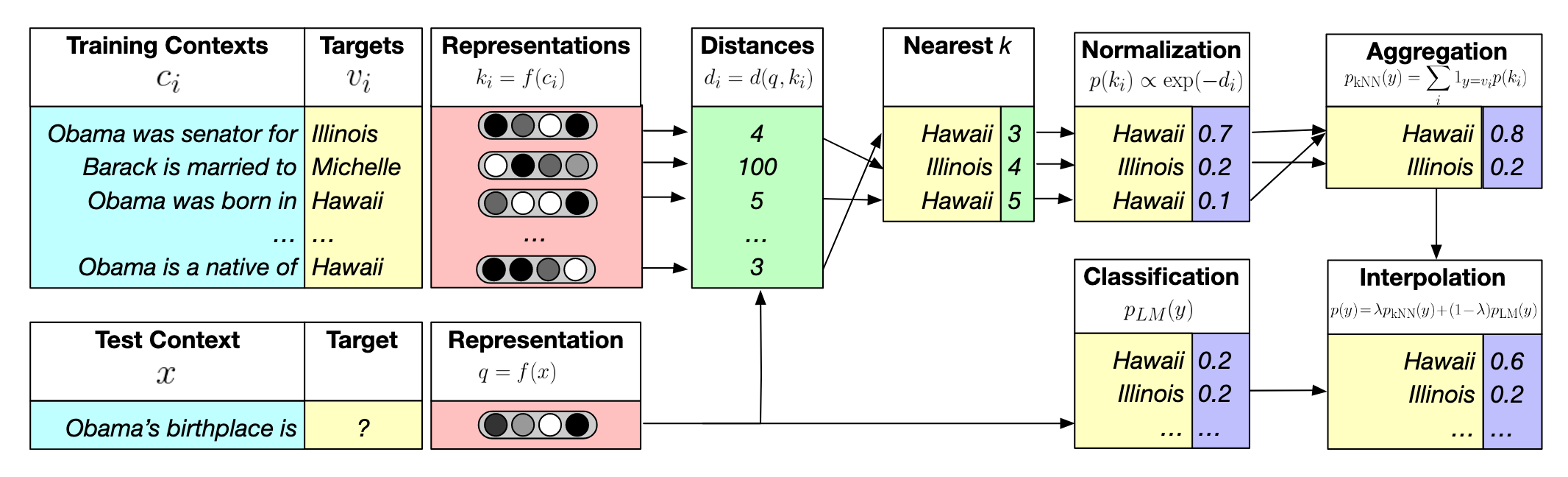
数据准备
使用 $k\texttt{NN-LM}$ 需要先对语料库的文本进行处理,分成下面几个步骤,下面我会结合一个详细的例子来进行说明,比如语料库里面有这么一个句子
Today is a good [day]这句子可以被分为 2 个部分
Today is a good day是上下文 $c_i$(Context),把这个上下文扔给 LLM,就可以得到一个向量表示 $f(c_i)$day是下一个 token $w_i$(Target)
这样就得到了一个 $(f(c_i),w_i)$ 的 pair,可以存储在 KV 数据库里面,在论文里叫做 Datastore
推理阶段
Info
KNN 算法我之前写过一篇博客介绍,在这里
那么在模型推理的时候如何使用这个 KV 数据库呢?假设用 $x$ 表示 LLM 的输入,那么步骤如下
- 用 LLM 生成它的向量表示 $f(x)$
- 用 $f(x)$ 作为 Query,在 KV 数据库里面用 KNN 算法找到最近的 $k$ 个邻居(用 $\mathcal N$ 表示)。换句话说,找和 LLM 输入 $x$ 最相似 $k$ 个上下文,注意每一个上下文都有下一个 token
- 假设邻居 $i$ 到 $f(x)$ 的距离是 $d_i$,$k$ 个邻居的距离就得到了一个距离向量数组 $[d_1, d_2,…,d_k]$,将距离取负然后做 Softmax 就得到了概率分布,这是关于距离的概率分布,但也可以转化为关于每个邻居背后的 token $w_i$ 的概率 $[p_1,p_2, p_3,…,p_k]$。注意这里可能不同邻居的下一个 token 是一样的,那么对应的概率要相加(可以看前面的图,有 2 个 Hawaii)
- 此时再把 Vocab $\mathcal V$ 的其他 token 的概率设置为 0,就得到了在 Vocab $\mathcal V$ 上的概率分布 $p_\texttt{kNN}(y|x)$,一个长度为 $|\mathcal V|$ 的向量
而 LLM 也会为输入 $x$ 输出下一个 token 的概率分布 $p_\texttt{LM}(y|x)$
引入一个超参数 $\lambda$ 综合这两个概率分布
$$ p(y|x)=\lambda p_\texttt{kNN}(y|x)+(1-\lambda)p_\texttt{LM}(y|x) $$
用这下一个 token 的概率分布预测下一个 token 即可
实验
用 FAISS 快速检索 KV 数据库中的邻居
距离的计算则采用欧几里得距离而不是向量内积,因为作者发现这个效果更好
根据实验结果,有如下几个发现(知识库指的就是 KV 数据库)
| 发现 | 索引 |
|---|---|
| 将 LLM 的训练数据作为知识库能降低 LLM 输出的困惑度 | Table 1 |
| 在小数据集上微调 LLM,并外挂一个大知识库,比直接在这个大知识库上做训练效果更好 | Table 3 |
| 最好的上下文表示是:LLM 的最后一个 transformer 层其中的 FFN 层的输入 | Figure 3 |
| 检索的邻居越多,效果越好 | Figure 4 |
| 如果知识库是同个领域的,那么就把 $\lambda$ 设置得小一点,反之就设置得大一点 |
Figure 5 |
kNN-LLM 的优缺点分析
在了解了 $k\texttt{NN-LM}$ 的原理之后,我们可以尝试理解一下它的优缺点
优点是 1
- 能够捕捉到文本中一些罕见模式,对 out-of-domain 的文本生成效果也比较好,这体现在 $k\texttt{NN}$ 和 $\texttt{LM}$ 的协同
- $k\texttt{NN}$ 可以捕捉到:上下文相似,下一个 token 一样,但 token 的含义不同
- $\texttt{LM}$ 可以捕捉到:上下文不同,下一个 token 一样
不足点是 1
- 空间开销大,因为给定语料库我们是为每个 token 构造 KV pair,所以 KV 数据库的大小跟跟 token 数量挂钩。所以在 Scalability 上 $k-\texttt{NN-LM}$ 存在比较大的问题
- 在模型输入和检索结果之间没有注意力的计算,这会降低模型的表现