What is Multi-Head Attention (MHA)

What’s Multi-Head Attention (MHA)

In last post I have explained how the self-attention mechanism works. Today let’s take a step further and explore multi-head attention (MHA), which is the full version of self-attention as described in the original paper¹. Since I have covered most of the foundation concepts in last post, this post will be short. :)

Previously, we mentioned that the self-attention mechanism has three import matrices.

$$ \mathbf Q,\mathbf K,\mathbf V\in\mathcal{R}^{n\times d} $$

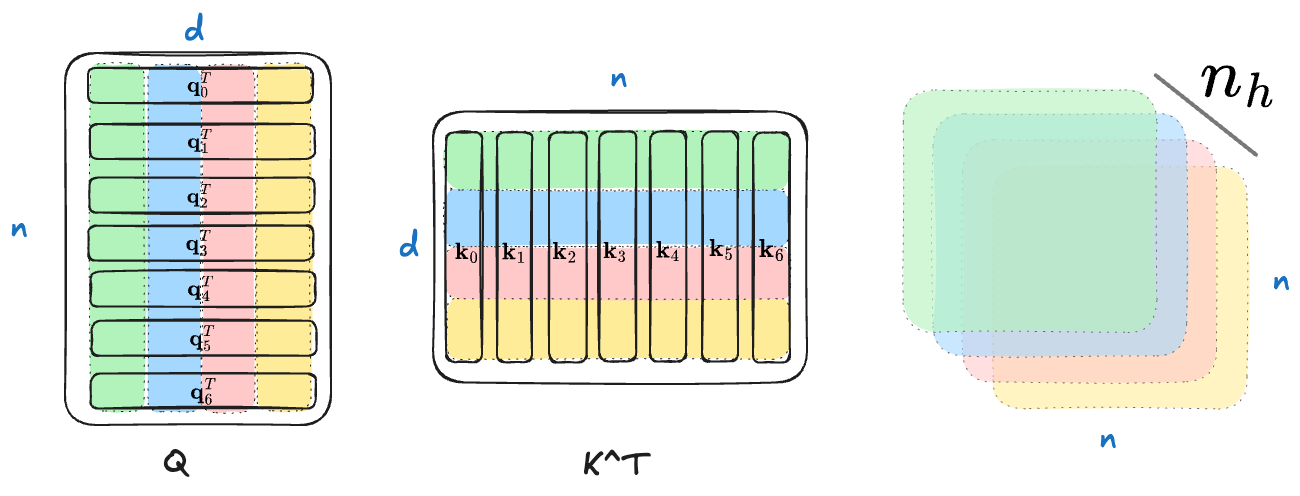
Let’s assume we want to use $n_h$ heads. The core idea of MHA is to split the query/key/value vector into $n_h$ parts, each of length $d_h=d/n_h$. The transformation changes the shape of the matrices to:

$$ \mathbf Q,\mathbf K,\mathbf V\in\mathcal{R}^{n_h\times n\times d_h} $$

Note that the $n_h$ is put in the first position of dimensions.

What are the benefits of introducing multi-head? In my opinion, the key to understanding MHA lies in analyzing matrix multiplication and observing how the shape changes. Before applying MHA, the attention score matrix is computed as

$$ \begin{split} \mathbf Q\in\mathcal{R}^{n\times d}\\ \mathbf K^T\in\mathcal{R}^{d\times n}\\ \mathbf Q\mathbf K^T\in\mathcal R^{n\times n} \end{split} $$

So we get an attention score matrix here.

After applying MHA, the equations become

$$ \begin{split} \mathbf Q\in\mathcal{R}^{n_h\times n\times d_h}\\ \mathbf K^T\in\mathcal{R}^{n_h\times d_h\times n}\\ \mathbf Q\mathbf K^T\in\mathcal R^{n_h\times n\times n} \end{split} $$

As a result, we obtain $n_h$ attention score matrices. To provide some intuition, I have drawn a diagram (assuming $n_h=4$). The computation occurs within the corresponding matrices of the same color, producing multiple attention score matrices.

For simplicity, let’s ignore the scaling factor $1/\sqrt d_h$ for now, then the final output of MHA is

$$ \texttt{softmax}(\mathbf Q\mathbf K^T)\mathbf V\in\mathcal R^{n_h\times n\times d_h} $$

Finally, we can reconstruct the output by reshaping ($\mathcal R^{n_h\times n\times d_h}\rightarrow\mathcal{R}^{n\times d}$).

Implementation

The implementation is straightforward, building upon the self-attention code from my last post. The key modifications are

• The target shape of bias is changed to (1, 1, block_size, block_size).
• The q, k, v matrices need to be reshaped.
• contiguous should be called before reshaping for attn @ v.

The complete code is shown below.

class MultiHeadAttn(nn.Module):
    def __init__(self, n_embd: int, block_size: int, n_heads: int):
        super().__init__()
        self.attn = nn.Linear(n_embd, 3 * n_embd)
        self.n_embd = n_embd
        self.n_heads = n_heads
        assert self.n_embd % self.n_heads == 0
        self.register_buffer(
            "bias",
            torch.tril(torch.ones(block_size, block_size)).view(
                1,
                1,
                block_size,
                block_size,
            ),
        )

    def forward(self, x):
        B, T, C = x.size()  # (batch_size, seq_len, n_embd)
        qkv = self.attn(x)  # qkv: (batch_size, seq_len, 3 * n_embd)
        q, k, v = qkv.split(self.n_embd, dim=2)  # split in n_embd dimension
        q = q.view(B, T, self.n_heads, C // self.n_heads).transpose(
            1, 2
        )  # q: (batch_size, n_heads, seq_len, n_embd)
        k = k.view(B, T, self.n_heads, C // self.n_heads).transpose(
            1, 2
        )  # k: (batch_size, n_heads, seq_len, n_embd)
        v = v.view(B, T, self.n_heads, C // self.n_heads).transpose(
            1, 2
        )  # v: (batch_size, n_heads, seq_len, n_embd)
        attn = (q @ k.transpose(-2, -1)) * (
            1.0 / math.sqrt(k.size(-1))
        )  # attn: (batch_size, n_heads, seq_len, seq_len)
        attn = attn.masked_fill(self.bias[:, :, :T, :T] == 0, -float("inf"))
        attn = F.softmax(attn, dim=-1)
        out = (attn @ v).transpose(1, 2).contiguous().view(B, T, C)

        return out

Wrap-up

To summarize, the essence of MHA lies in the dimensionality. With MHA, although the query/key/value vectors are shortened ($d\rightarrow d_h$), we obtain more attention score matrices ($1\rightarrow n_h$). If each attention score matrix captures a distinct pattern, then MHA effectively captures multiple patterns, leading to improved performance :)

Ref