Boyer-Moore Majority Voting Algorithm Explained

Intro

Today I coded the Leetcode 169. Majority Element again. I vaguely remember what the optimal solution is called Boyer-Moore Majority Voting Algorithm. However, I have no idea what is except for its name. So I plan to systematically learn the principle of this algorithm and summarize it to write this blog. I once heard that:

If you want to master something, teach it :)

So, I’m here today to share this algorithm with you, and try to teach you this method in plain language, so let’s get started :)

Let’s start from the baselines

If you have never heard of the Boyer-Moore Majority Voting Algorithm, how would you try to solve this problem? I think these methods should come to your mind:

1. Exchange space for time efficiency, that is, we use a hash table to record the number of occurrences of each element in the array, and then we check our hash table again to find the number of occurrences that is greater than $\lfloor n/2\rfloor$. Apparently, the time complexity and space complexity are both $O(n)$
2. Try to sort the array, because the element we are looking for exceeds the half-length of the array, which means it must appear in the middle of the array after sorting. However, although the space complexity is $O( 1)$, the time complexity is still greater than $O(n)$. For example, if you use quicksort, the time complexity is $O(nlogn)$

So is there a way to achieve a time complexity of $O(n)$ and a space complexity of $O(1)$? That is to combine the advantages of the above two methods. Yes, the answer is the Boyer-Moore Majority Voting Algorithm!

Boyer-Moore Majority Voting Algorithm

Problem description: Suppose our array has $n$ elements, and we want to find the elements that appear more than $\lfloor n/2\rfloor$ times.

Algorithm:

1. Choose one of these $n$ elements as a candidate and record its votes as votes = 1.

2. At this point there are $n-1$ elements in our array, we take out one element each time (denoted as current), and repeat the following steps (a total of n-1 times)

   1. Compare it to our current candidate, if they have the same value, then votes++, which is an affirmative vote
   2. If their values are different, votes--, that is, a dissenting vote. If we get votes = 0 at this time, then candidate <- current, which means that we make current the new candidate, and reset votes = 1

3. The final value of the candidate is maybe the element that appears more than half of the times we want, at this point, we have to traverse the array again to check if it is

After reading the above algorithm procedure, you may be as confused as I was. Why do we finally find the elements with more than half of the occurrences? In order to answer this question, we need to understand this:

💡 If there is an element that appears more than $\lfloor n/2\rfloor$ times, then the other elements in the array must appear less than $\lfloor n/2\rfloor$ in all.

Why it is useful? ⬆️

Because what this algorithm does is actually voting:

• It can be an affirmative vote, which is equal to the occurrences times of this element
• It can be a dissenting vote, which is equivalent to canceling one affirmative vote

But the number of votes (affirmative votes) for the elements that appear more than $\lfloor n/2\rfloor$ times > the remaining all that are not (dissenting votes) is always to be true, so no matter what, the final winner will always be the element we are searching(if it exists) :)

To get a intuitive understanding ⬇️

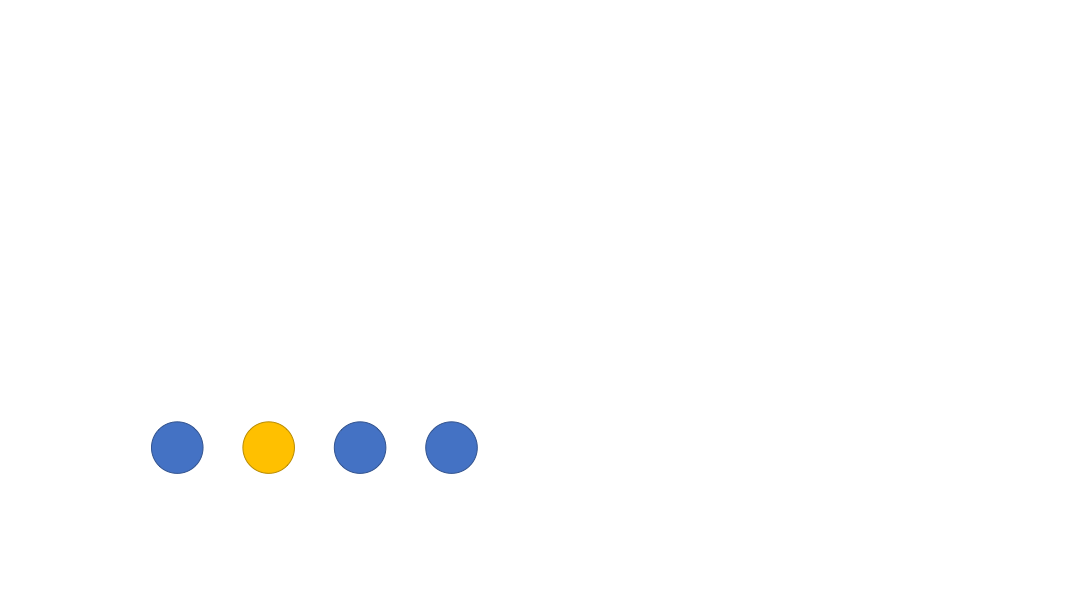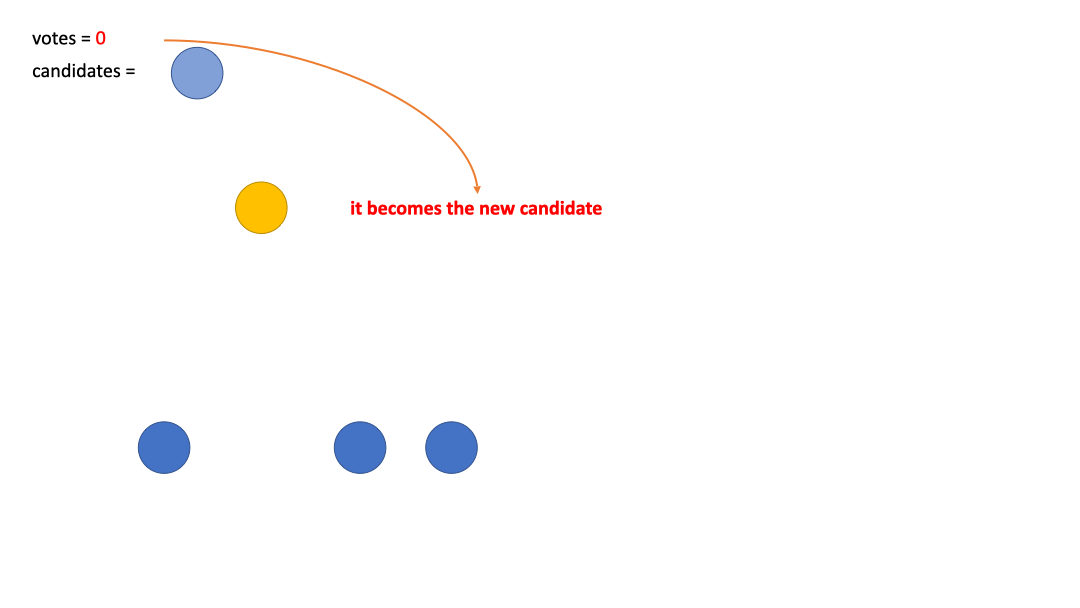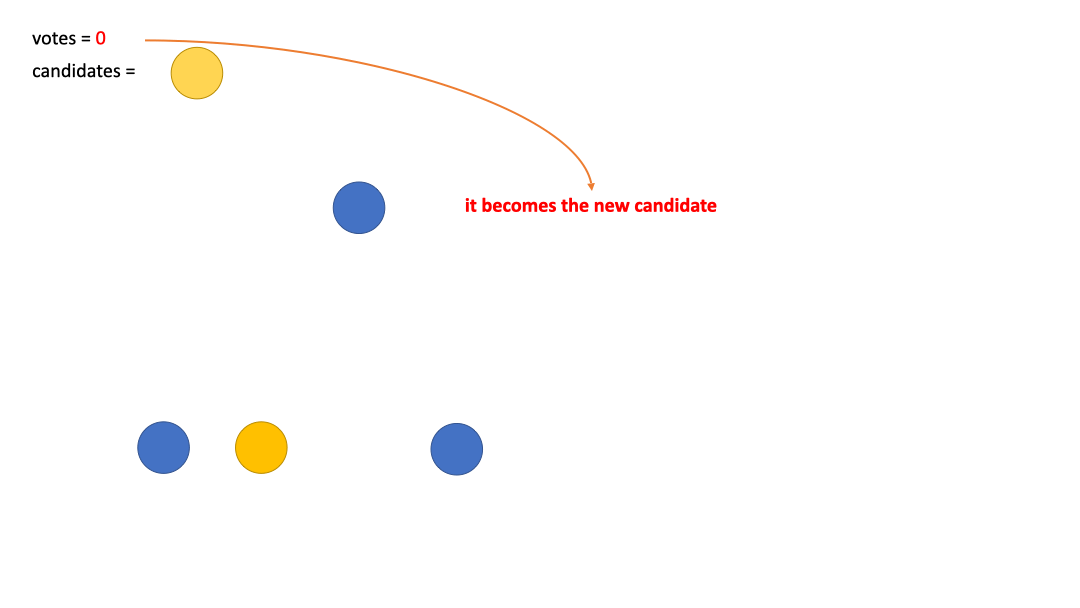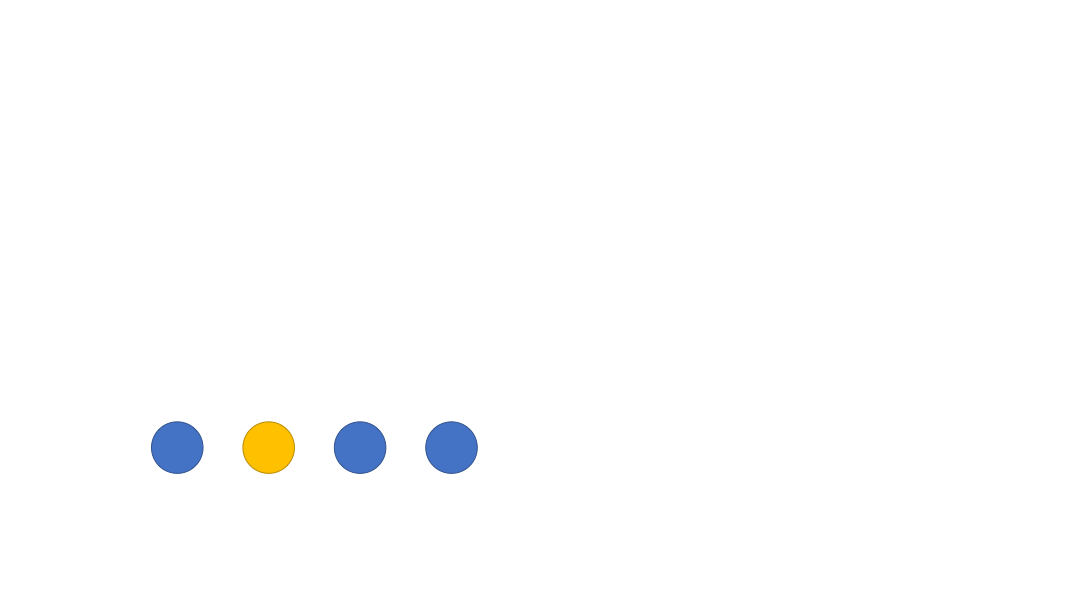
Code

class Solution {
    public int majorityElement(int[] nums) {
        if (nums.length < 2) {
            return nums[0]; 
        }
        int candidates = nums[0];
        int votes = 1;
        // step 1. start to vote
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != candidates) {
                votes -= 1;
                if (votes == 0) {
                    candidates = nums[i];
                    votes = 1;
                }
            } else {
                votes += 1;
            }
        }
        // step2. check
        int occurs = 0;
        for (var val: nums) {
            if (candidates == val) {
                occurs += 1;
            }
        }
        if (occurs >= nums.length / 2) {
            return candidates;
        } else {
            return -1;
        }
    }
}

FAQ

Q: Why do you need a second round of for-loop? Can we just check the votes directly?

A: No, first of all, the element that “occurs more than $\lfloor n/2\rfloor$ times” does not always exist. e.g. [1,2,3]. In addition, even if it exists, after traversing the array for the first time, the votes does not necessarily equal to it real occurrence times. e.g. [1, 2, 2, 2, 3]