From Basic Block to Control Flow Graph

Basic Block (BB)

What’s BB

flowchart
    subgraph tac [Three-Address Code]
        subgraph bb1 [Basic Block 1]
            direction TB
            instruction1
            instruction2
        end
        subgraph bb2 [Basic Block 2]
            direction TB
            instruction3
            instruction4
            instruction5
        end
    end

After getting the Three-Address Code representation of the program, we can take a step further to group the instructions of the Three-Address Code to different BBs, which is illustrated in the above diagram. Each BB contains maximal continuous instructions of Three-Address Code and it should follow these rules:

• It should contains onlye one entry, which is the first instruction of BB.
• It should contains onlye one exit, which is the last instruction of BB.

How to get BB

Input: All instructions in the Three-Address Code of the program.

Output: a BB list.

Algorithm：

1. Find all the leaders, where the leader refers to the entry of each BB.
   1. The first instruction of input is a leader.
   2. Any target label (instruction) of jump instruction (conditional or unconditional) is a leader.
   3. Any instruction follows a jump instruction (conditional or unconditional) is a leader.
2. Just split the input by leaders and you will get a BB list.
3. Optional: Change all target label(s) of jump instruction (conditional or unconditional) from instruction to BB label, for each BB has only one entry and one exit.

Use LLVM IR as an example

Let’s use the same example in previous post. We want to find the BBs of the following C/C++ code (main.cpp).

int main() {
    int sum = 0;
    for (int i = 0; i < 10; i++) {
        sum += i;
    }
    return 0;
}

Let’s use clang to get the LLVM IR with the following commands:

$ clang -S -emit-llvm main.cpp

I have extracted all the instructions for you and added indices to each instruction in the (i) form.

(1) %1 = alloca i32
(2) %2 = alloca i32
(3) %3 = alloca i32
(4) store i32 0, ptr %1
(5) store i32 0, ptr %2
(6) store i32 0, ptr %3
(7) br label (8)
(8) %5 = load i32, ptr %3
(9) %6 = icmp slt i32 %5, 10
(10) br i1 %6, label (11), label (20)
(11) %8 = load i32, ptr %3
(12) %9 = load i32, ptr %2
(13) %10 = add nsw i32 %9, %8
(14) store i32 %10, ptr %2
(15) br label (16)
(16) %12 = load i32, ptr %3
(17) %13 = add nsw i32 %12, 1
(18) store i32 %13, ptr %3
(19) br label (8)
(20) ret i32 0

Based on the previously mentioned algorithm, we need to find all the leaders first

1. The first instruction of input is a leader. Therefore, (1) is a leader.
2. Any target label (instruction) of jump instruction (conditional or unconditional) is a leader. Therefore, (8), (11), (20), (16) are leaders.
3. Any instruction follows a jump instruction (conditional or unconditional) is a leader. Therefore, (8), (11), (16), (20) are leaders

Let’s deduplicate all the leaders and we should get all the unique leaders: (1), (8), (11), (16), (20). Now we get the following BBs.

(1) %1 = alloca i32
(2) %2 = alloca i32
(3) %3 = alloca i32
(4) store i32 0, ptr %1
(5) store i32 0, ptr %2
(6) store i32 0, ptr %3
(7) br label (8)

(8) %5 = load i32, ptr %3
(9) %6 = icmp slt i32 %5, 10
(10) br i1 %6, label (11), label (20)

(11) %8 = load i32, ptr %3
(12) %9 = load i32, ptr %2
(13) %10 = add nsw i32 %9, %8
(14) store i32 %10, ptr %2
(15) br label (16)

(16) %12 = load i32, ptr %3
(17) %13 = add nsw i32 %12, 1
(18) store i32 %13, ptr %3
(19) br label (8)

(20) ret i32 0

Is it correct? We can compare it with the origin output of clang, and it’s clear that we make it right :)

define noundef i32 @main() #0 {
0:  ; this line is added by me to make it more explicit
  %1 = alloca i32
  %2 = alloca i32  ; %2 is sum
  %3 = alloca i32  ; %3 is i
  store i32 0, ptr %1
  store i32 0, ptr %2       ; sum = 0
  store i32 0, ptr %3       ; i = 0
  br label %4               ; jump to %4

4:                                                ; preds = %11, %0
  %5 = load i32, ptr %3           ; load i
  %6 = icmp slt i32 %5, 10        ; %6 = check if i < 10
  br i1 %6, label %7, label %14   ; conditional jump based on if %6 is true

7:                                                ; preds = %4
  %8 = load i32, ptr %3     ; i
  %9 = load i32, ptr %2     ; sum
  %10 = add nsw i32 %9, %8  ; temp = sum + i
  store i32 %10, ptr %2     ; sum = temp
  br label %11              ; jump to %11

11:                                               ; preds = %7
  %12 = load i32, ptr %3     ; i
  %13 = add nsw i32 %12, 1   ; temp = i++
  store i32 %13, ptr %3      ; i = temp
  br label %4                ; jump to %4

14:                                               ; preds = %4
  ret i32 0                  ; return 0
}

Control Flow Graph (CFG)

What’s CFG

CFG is one type of intermediate representation (IR), which is the basics of static program analysis. It consists of

• Node: Usually a node is a BB, but sometimes it may be an instruction of Three-Address Code¹
• Edge: The direction of the edge indicates the transfer of control, or in other words, the code may continue executing along this edge.

We can plot the CFG with a mermaid:

flowchart TB
    subgraph CFG [Control Flow Graph]
        bb1(Basic Block 1)
        bb2(Basic Block 2)
        bb3(Basic Block 3)
        bb4(Basic Block 4)
        bb1 --> bb2 & bb3
        bb2 & bb3 --> bb4
    end

How to get CFG

Input: A BB list. Let’s use $B_i$ to represent the $i$-th BB.

Output: A CFG

Algorithm:

• If $B_j$ is the target of jump instruction (conditional or unconditional) of $B_i$, then connect $B_i$ to $B_j$ (denoted as $B_i\rightarrow B_j$).
• If $B_j$ follows $B_i$ and the last instruction of $B_i$ is not a unconditional jump, then connec $B_i$ to $B_j$ (denoted as $B_i\rightarrow B_j$).

Use LLVM IR as an example

0:  ; this line is added by me to make it more explicit
  %1 = alloca i32
  %2 = alloca i32  ; %2 is sum
  %3 = alloca i32  ; %3 is i
  store i32 0, ptr %1
  store i32 0, ptr %2       ; sum = 0
  store i32 0, ptr %3       ; i = 0
  br label %4               ; jump to %4

4:                                                ; preds = %11, %0
  %5 = load i32, ptr %3           ; load i
  %6 = icmp slt i32 %5, 10        ; %6 = check if i < 10
  br i1 %6, label %7, label %14   ; conditional jump based on if %6 is true

7:                                                ; preds = %4
  %8 = load i32, ptr %3     ; i
  %9 = load i32, ptr %2     ; sum
  %10 = add nsw i32 %9, %8  ; temp = sum + i
  store i32 %10, ptr %2     ; sum = temp
  br label %11              ; jump to %11

11:                                               ; preds = %7
  %12 = load i32, ptr %3     ; i
  %13 = add nsw i32 %12, 1   ; temp = i++
  store i32 %13, ptr %3      ; i = temp
  br label %4                ; jump to %4

14:                                               ; preds = %4
  ret i32 0                  ; return 0

The example here comes from a previous example in BB. Note that we have already computed the BBs. Now we just need to figure out how to make connections between BB. Based on the algorithm, we can try:

• Check all the jump instruction
  • %0 will jump to %4, so there exists the edge %0 -> %4.
  • %4 might jump to %7, %14, so there exist the edges %4 -> %7 and %4 -> %14.
  • %7 will jump to %11, so there exists the edge %7 -> %11.
  • %11 will jump to %4, so there exists the edge %11 -> %4.
• Check all the unconditional jump instruction
  • %7 follows %4 and %4 ends with a conditional jump instruction, so there exists the edge %4 -> %7

How do we verify if our answer is correct? The answers lie in the comment of LLVM IR.

0:  ; this line is added by me to make it more explicit
... ; omit
4:                                                ; preds = %11, %0
... ; omit
7:                                                ; preds = %4
... ; omit
11:                                               ; preds = %7
... ; omit
14:                                               ; preds = %4
... ; omit

From the comments, we know the predecessor of %4 are %11 and %0, which is consistent with our answer. Following the same verification manner, we ensure that our answer is correct.

Finally, we can exploit clang and opt to dump the CFG.

$ clang -Xclang -disable-O0-optnone -S -emit-llvm main.cpp -o main.ll
$ opt -passes='dot-cfg' main.ll 
$ dot -Tpdf .main.dot -o result.pdf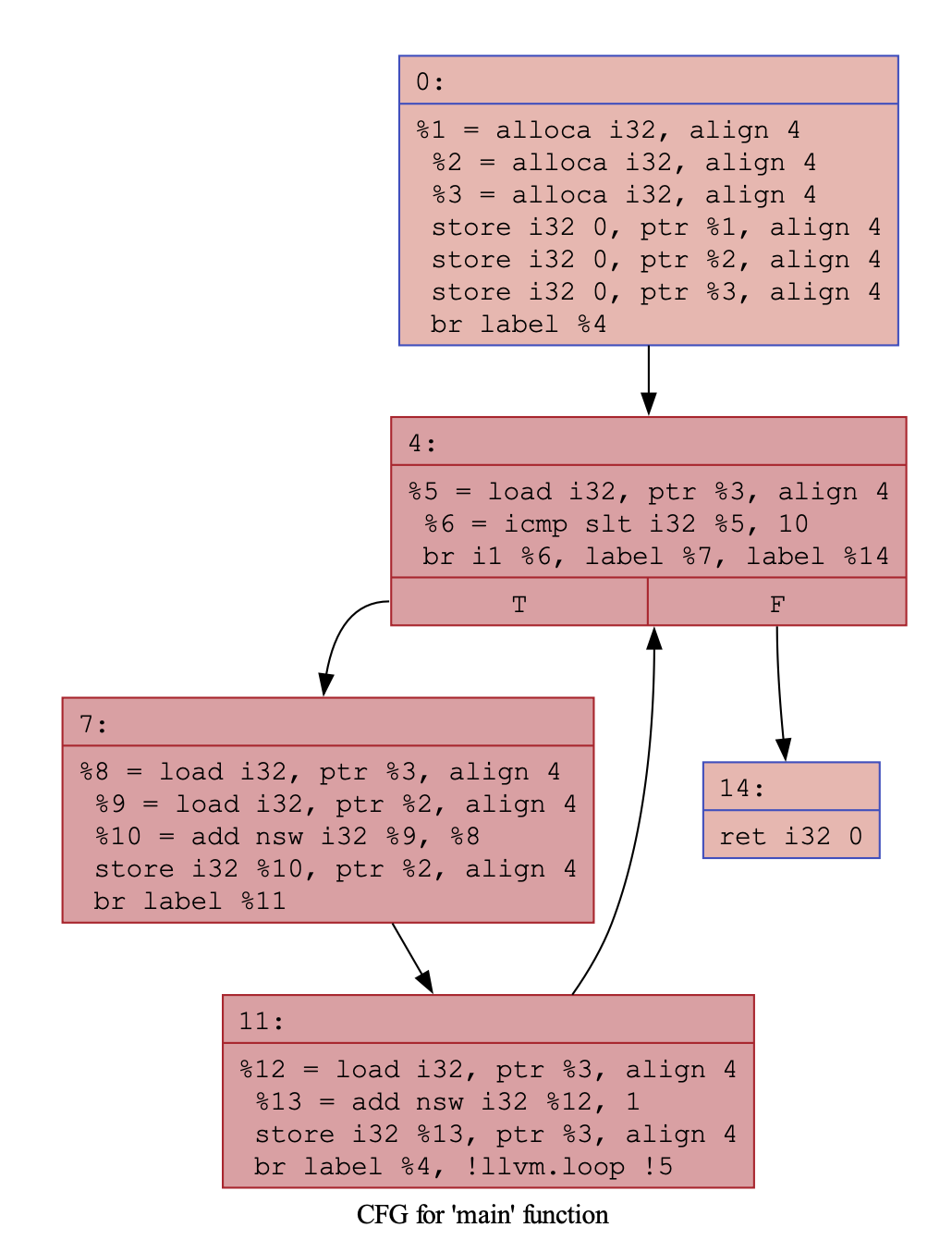

Wrap-up

That’s all for this post. Using the same example, we have connected the dots from the Three-Address code to the Basic Block, and then to CFG. Once we have CFG, subsequent program analysis like data flow analysis becomes much easier.

Ref