Posts Tags Categories About

How to memorize the Red-black tree

MartinLwx  included in  category Data-Structure
     2269 words  11 minutes 

If you are attracted by the title of this blog, I believe you may agree with me: The process of memorizing the insertion and deletion operations of the Red-black tree can be incredibly arduous. It entails keeping track of complex tree rotations and the necessity to recolor nodes as required. I once read the renowned Introducing to Algorithms written by the CLRS. However, there are so many cases to remember and I quickly get overwhelmed.

Of course, the best way to remember something is always to understand it. Recently, when I saw the slides for Stanford’s CS166 Advanced Data Structures course. It seems like I finally understand the Red-black tree - the Red-black tree is an isometry of 2-3-4 tree. They represent the structure of 2-3-4 trees in a different way1. So how can this help us? Well, We can deduce the changes in shape and color in a Red-black tree by observing the changes in the corresponding 2-3-4 tree.

Before we begin, I assume that you are familiar with the following:

  • You know the definitions of a 2-3-4 tree or B-tree. A 2-3-4 tree is a type of B-tree. You need to know how to perform deletion and insertion operations on a 2-3-4 tree, when nodes overflow or underflow, and how to handle these cases
  • You know how to insert and delete nodes in a binary search tree(BST) because a Red-black tree itself is a BST that ensures a height of $O(log n)$. You should already know how to find the insertion position and determine which node to delete in BST
  • You need to understand the definitions of Red-black trees and 2-3-4 trees. You should understand the properties of Red-black trees and which properties can be violated during node insertion and deletion

Most importantly, you don’t need to memorize the rotations and color changes in Red-black trees because once you grasp the techniques I’m going to discuss today, you can establish an intuitive connection between operations on Red-black trees and operations on 2-3-4 trees

There are 3 possible node types in a 2-3-4 tree:

  • 2-node, 2 children with 1 key
  • 3-node, 3 children with 2 key
  • 4-node, 4 children with 3 key

The node mappings tell us how to map a node in a 2-3-4 tree to nodes in the corresponding Red-black tree and vice versa. Note that all the structures of a Red-black in the following image start from a black node. We will use the node mappings extensively later.

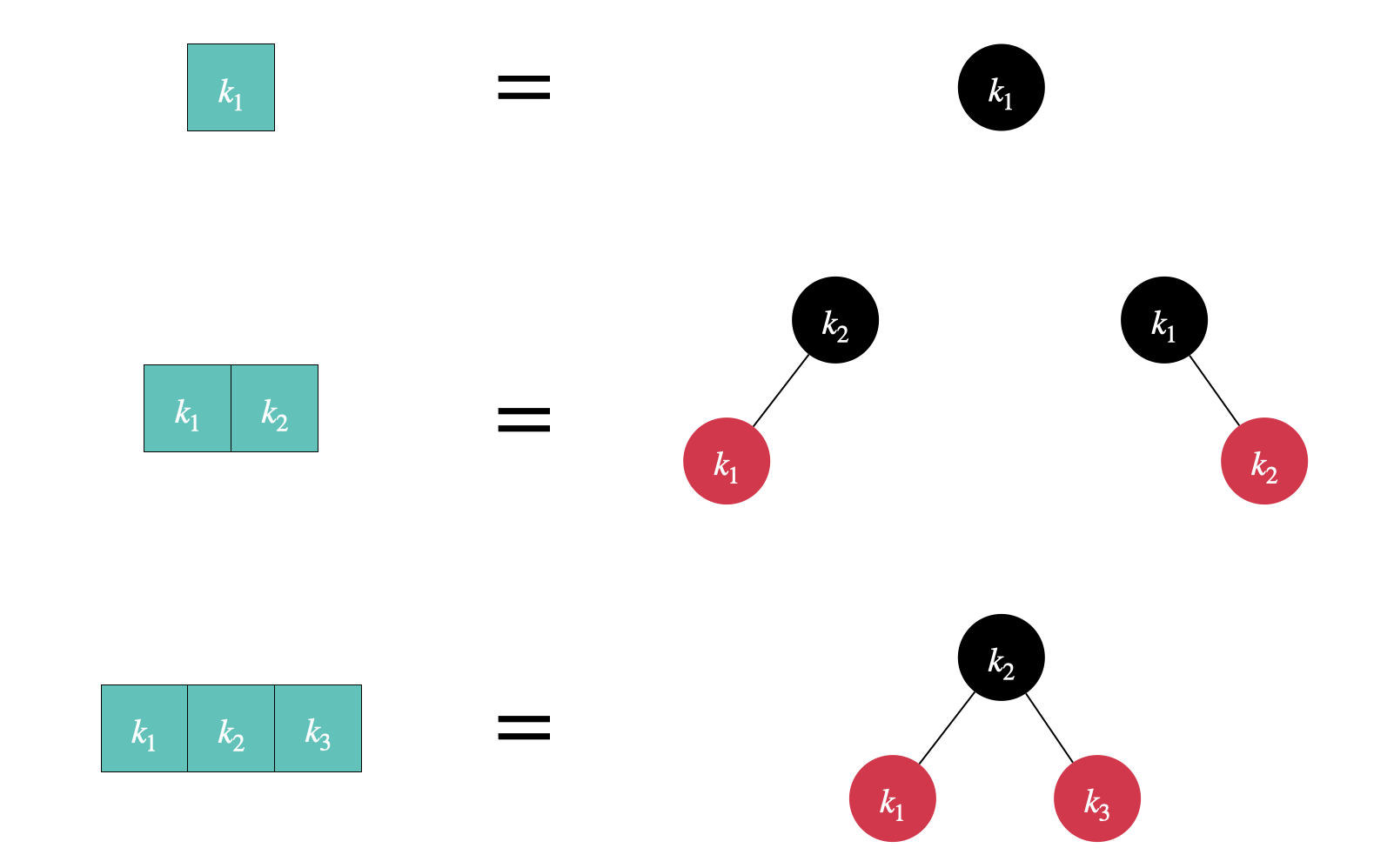
LHS: 2/3/4-node, RHS: the corresponding node structures

LHS: 2/3/4-node, RHS: the corresponding node structures

Let’s recap how to insert a node in a Red-black tree:

  1. Red-black trees are BSTs, so initially, we use the method of inserting nodes in a BST to find the appropriate position for insertion
  2. If the newly inserted node becomes the root node (i.e., the original Red-black tree is empty), then the newly inserted node is colored black. In other cases, it is colored red. This is because one of the properties of Red-black trees states that every path from any node to its leaf nodes contains an equal number of black nodes. By coloring the newly inserted node in red, we can maintain this property. We will only consider the case where the newly inserted node is colored red later

If the newly inserted node is red, it means that it may violate another property of the Red-black tree: there cannot be two consecutive red nodes. Red-black trees solve this problem by using tree rotations and node recoloring 🎨, but the rules can be complex and difficult to remember

Before showing specific examples, let’s summarize the general approach to insertion:

  • Insert this new node and color it red
  • Transform the “violating part” of the Red-black tree into an equivalent form on a 2-3-4 tree
  • Consider how to handle the equivalent form on the 2-3-4 tree
  • After handling it on the 2-3-4 tree, transform it back to a Red-black tree. At this point, the shape and color are determined

💡 To help readers understand how to transform between 2-3-4 tree and Red-black tree, I have used a colored transparent box to highlight the equivalent parts before and after the transformation

💡 I chose to use specific numerical values instead of abstract symbols because it provides a more intuitive understanding and makes it easier for readers to find connections between 2-3-4 tree and Red-black tree

A trivial case woudl be, the newly insertion node’s parent node is black. By the definition of the Red-black tree, we know we don’t need to change anything

Next, let’s consider a slightly more complex scenario where the parent node of the newly inserted node is red. Red-black trees do not allow such a situation to occur. In this case, the newly inserted node may or may not have an uncle node. Let’s first consider the scenario where it does not have an uncle node. We can easily draw the following possible forms:

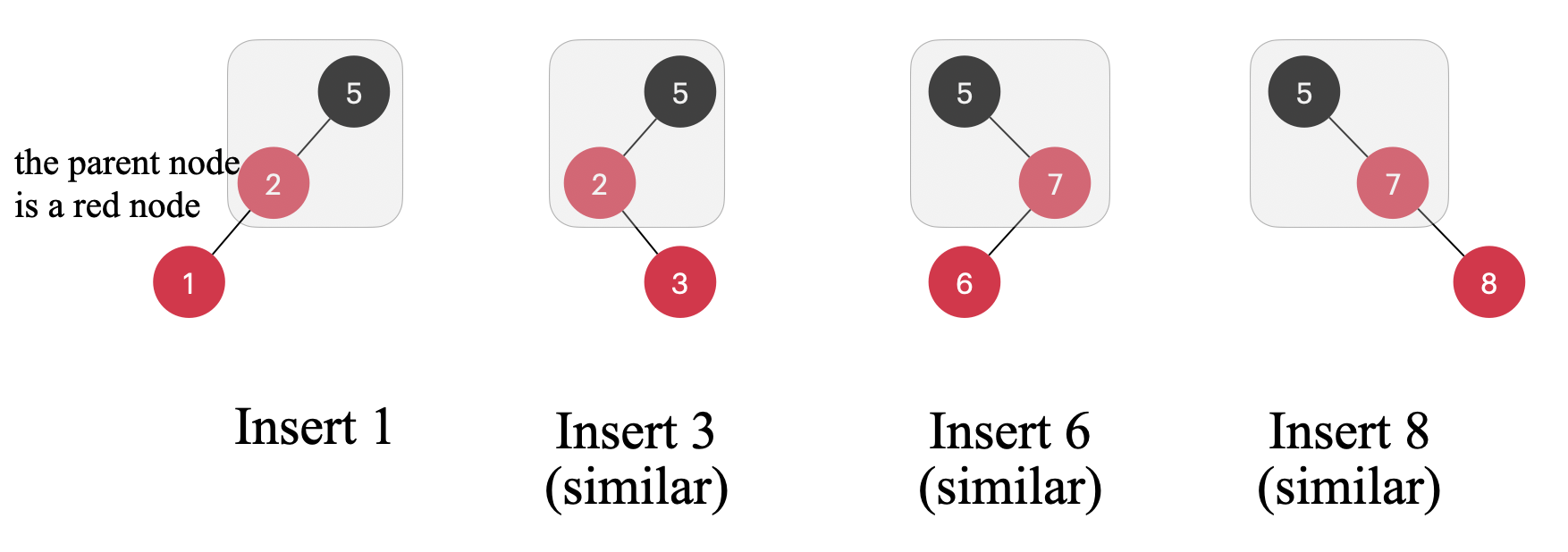
Please note that all of these forms are equivalent. Below, I will demonstrate how to operate the first example shown in the above diagram

💡 In the subsequent discussions of other scenarios, they may also have equivalent forms. However, the methods are generally similar, so I will pick one example to explain each time.

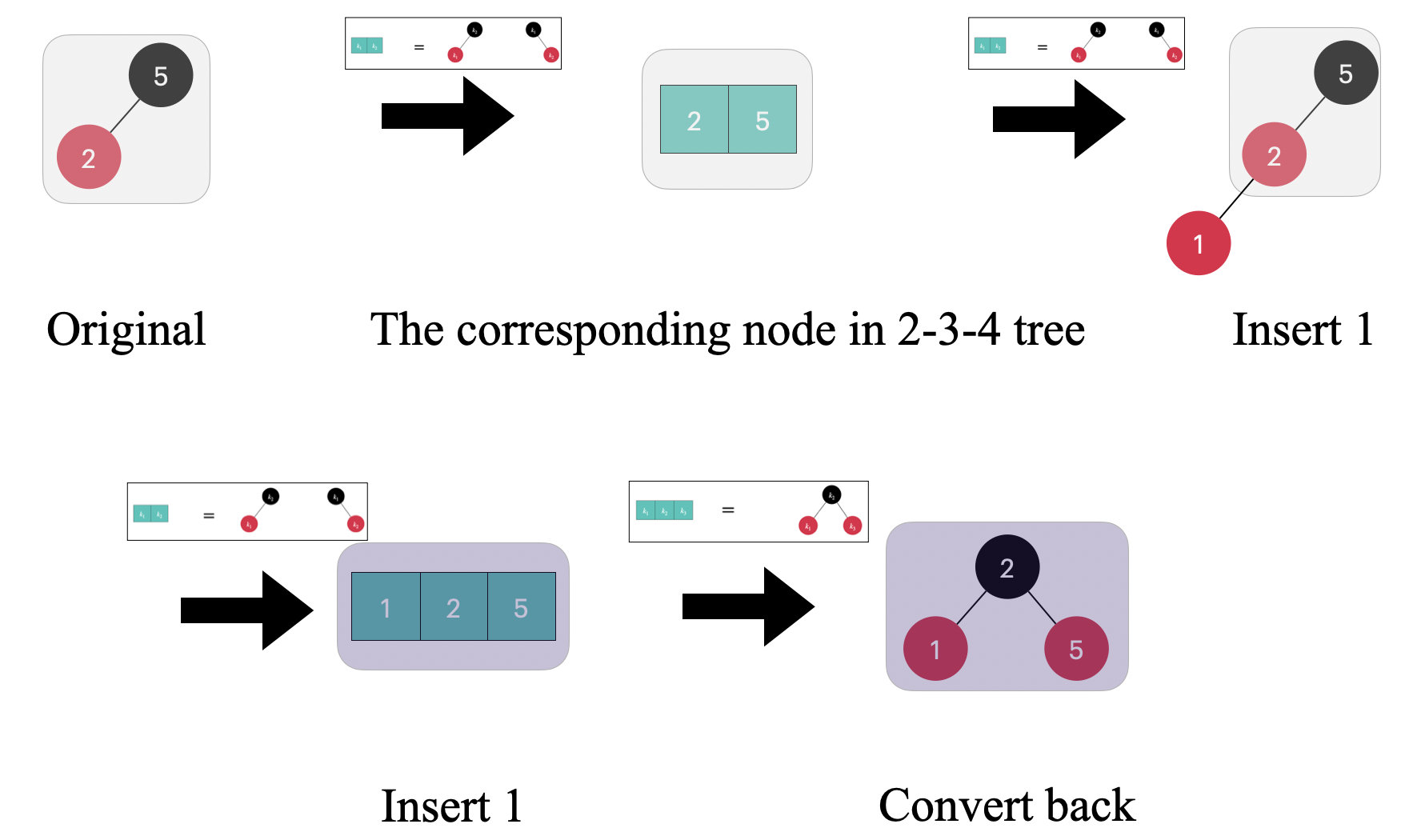
Based on the node mappings mentioned earlier, the Red-black tree before insertion corresponds exactly to a 3-node on the 2-3-4 tree. Then, we insert the node 1 into the Red-black tree. At the same time, we perform the insertion operation on the 3-node, resulting in a 4-node. The 4-node satisfies the requirements of a 2-3-4 tree, so there is no need to split the node. At this point, we can transform it back into a Red-black tree based on the node mappings

At this point, you may feel that the 2-3-4 tree doesn’t bring much convenience because a simple right rotation and recoloring are not complex tasks in this case. However, as the scenarios become more complex, you will find that the perspective from the 2-3-4 tree can be much easier to comprehend🤔️.

Now let’s consider a more complex scenario where the uncle node exists, which can be either black or red

Let’s first take a look at one of the possible cases when the uncle node is black

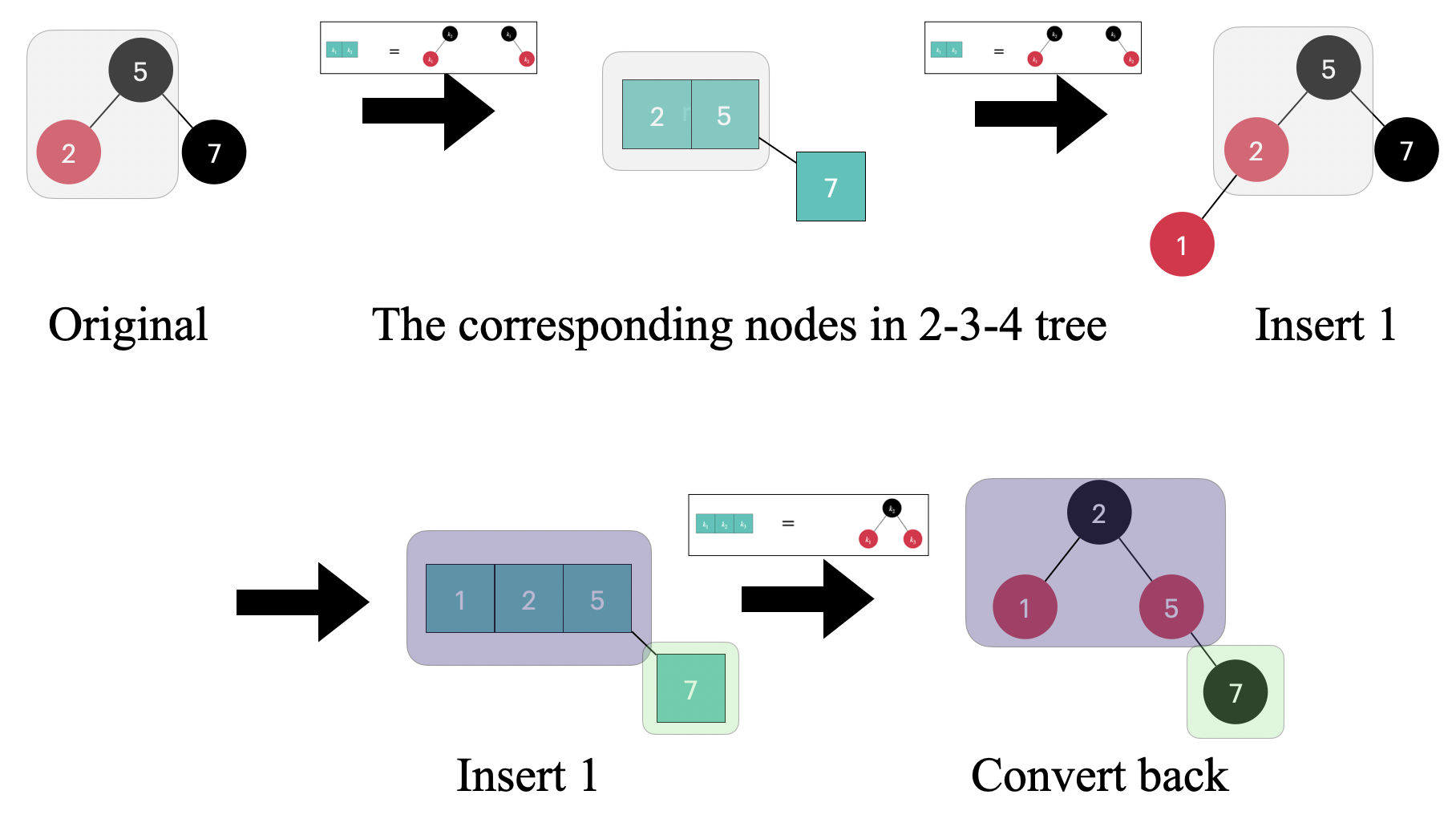
Based on the node mappings, we can map the 2, 5 nodes in the Red-black tree to a 3-node on the 2-3-4 tree, while the 7 node on the Red-black tree maps to a 2-node. When we insert 1 into the Red-black tree, we also insert 1 into the 3-node consisting of 2 and 5. The resulting 1, 2, 5 is mapped to a black node with two red children according to the rules. The 7 node is mapped as a black node

But what if the uncle node is red? For example, in the case shown below.

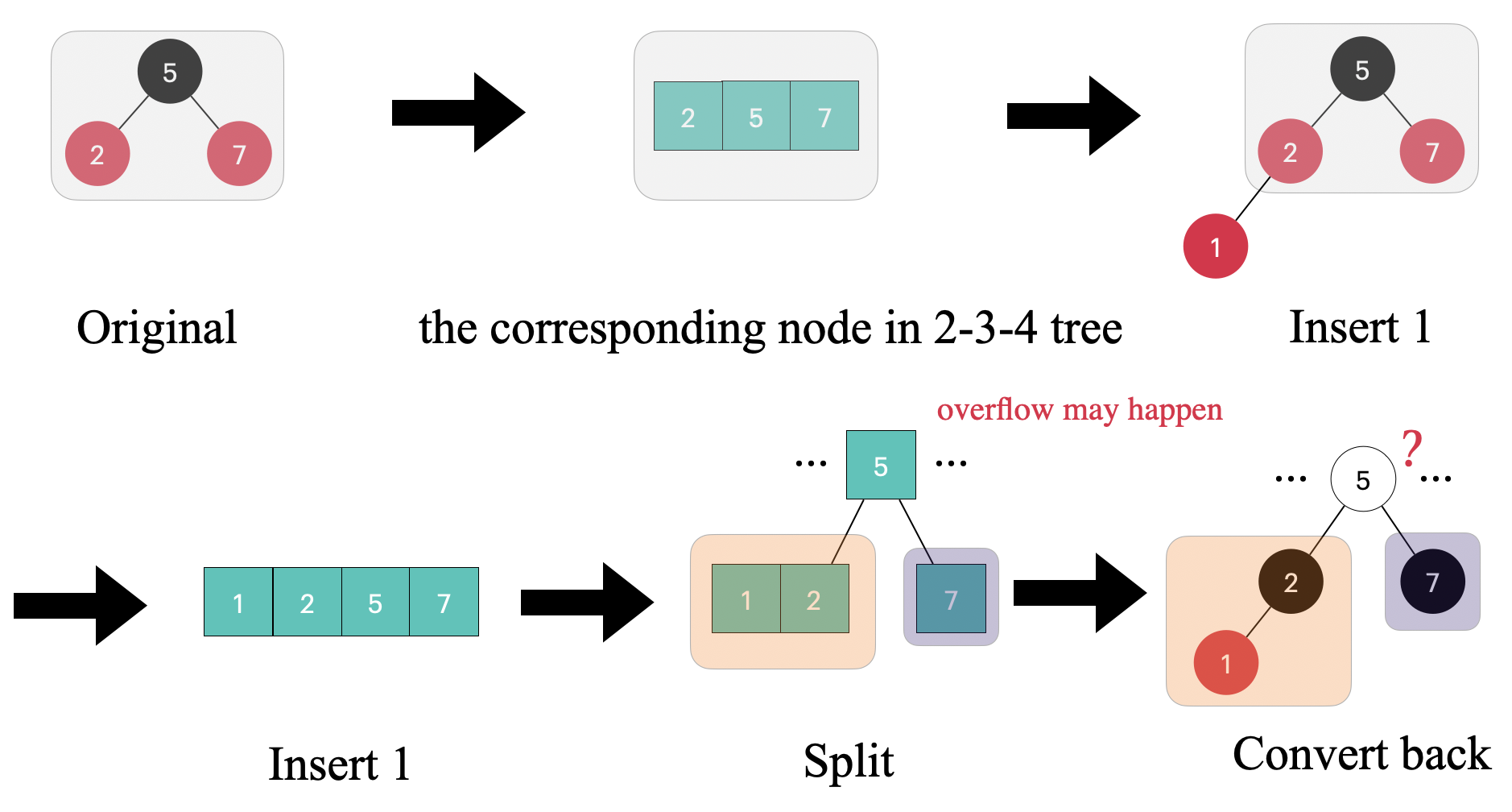
This case will be slightly more complex. Because after inserting 1 into the equivalent 2-3-4 tree, we need to perform a split operation on 1, 2, 5, 7. This means that we need to insert the node 5 into the parent node. *Since we don’t know the specific state of the parent node, the ellipses(...) are used to represent the nodes on both sides of 5. Inserting a node into the parent node in the 2-3-4 tree may also cause the parent node to overflow, and in the worst case, we need to modify all the way back

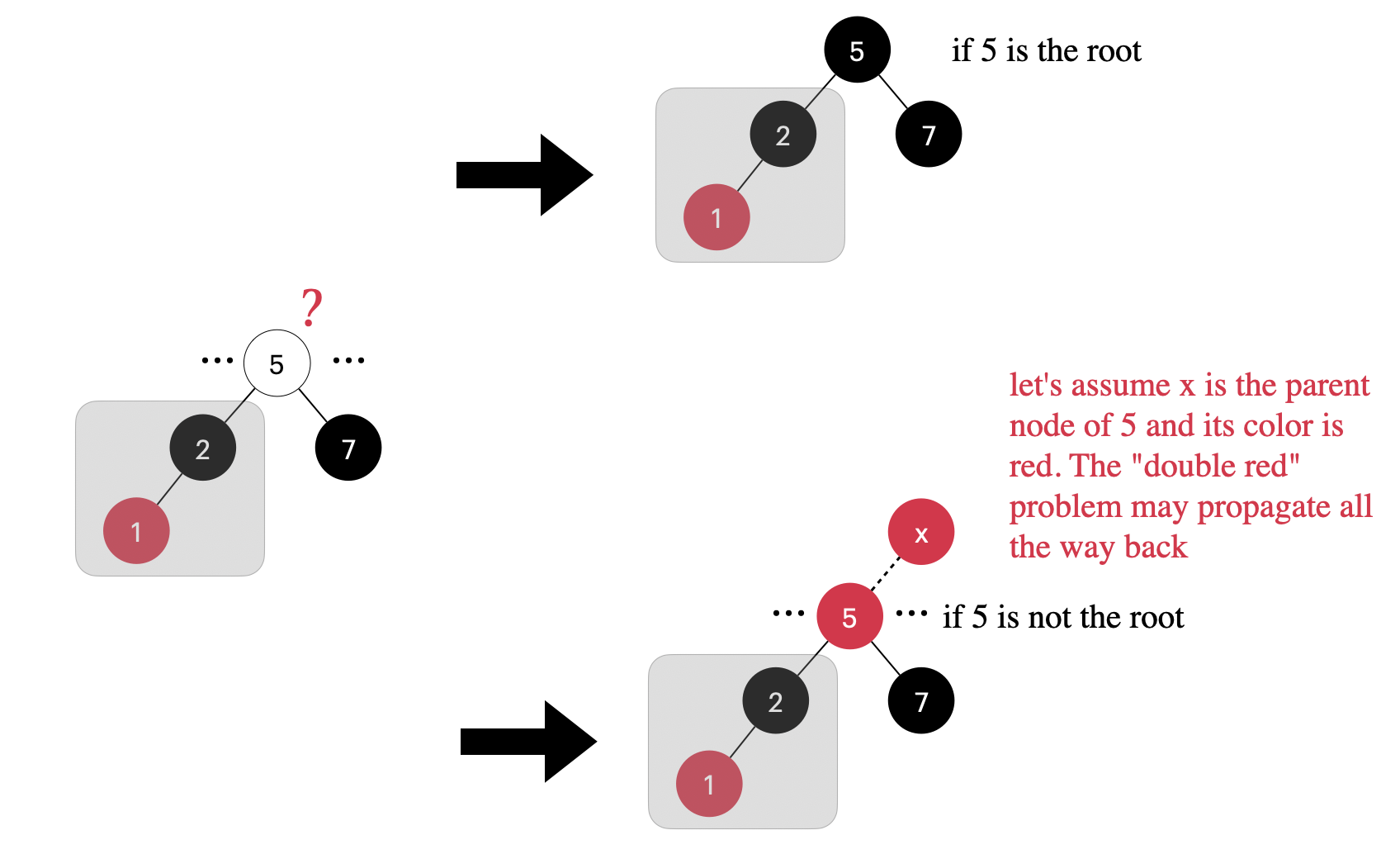
Additionally, it’s important to note that the grandparent node of the newly inserted node should be red. In the example, node 5 is the grandparent of the newly inserted node 1. This ensures that every path from any node to its leaf nodes contains the same number of black nodes. However, there is one exception, which is when the grandparent node is the root node of the Red-black tree. In that case, it should be black. The following diagram clearly shows these two possibilities.

Let’s recap how to perform node deletion in a Red-black tree:

  1. Following the procedure of deleting a node in a BST, find the node to be deleted. Let’s assume it is node z
  2. Based on the color of node z, we can distinguish the following two cases:
    1. z is red. Deleting a red node is relatively straightforward because it doesn’t break the properties of the Red-black tree. We won’t delve into this case here.
    2. z is black. Deleting a black node may potentially break the property of the Red-black tree that requires every path from any node to its leaf nodes to contain the same number of black nodes. In the Red-black tree, encountering this case still requires tree rotations and node recoloring🎨 to resolve the issue. The following discussion primarily focuses on this scenario

💡 Based on the deletion procedure of BST, we know that the node z to be deleted does not have a left child. If It has a right child, we will denote it as y

💡 The yellow node represents the unknown color or is irrelevant

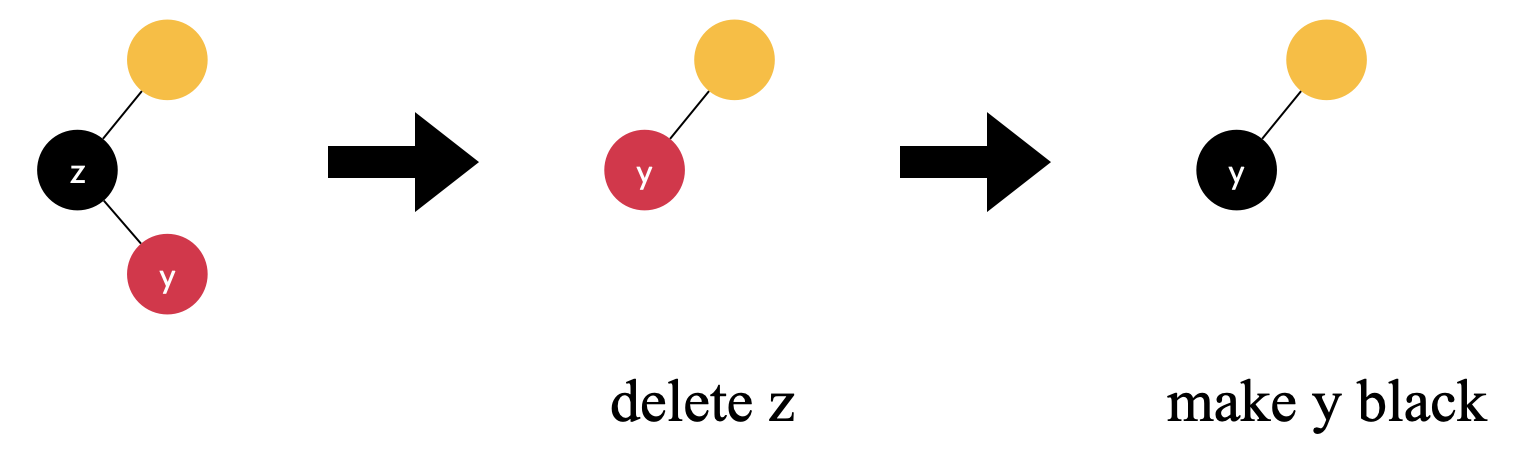
Delete the black z and replace z with red y

Let’s temporarily replace the black z with the black y, and mark y as a “double black” node. *In the diagram, a black node with a circular border represents a “double black” node2

💡 In the context of a Red-black tree, “double black” means that we need two black nodes on this side. In the context of a 2-3-4 tree, it corresponds to an underflow situation after you delete a key in a 2-node

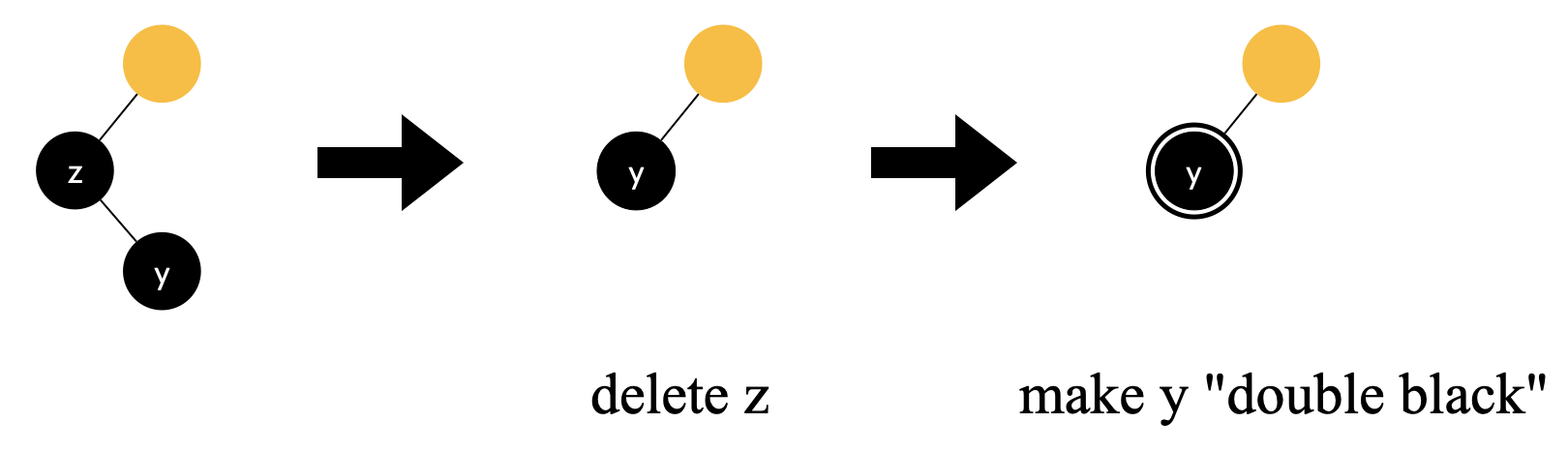
Delete the black z and replace z with black y, and mark y as “double black”

Now we need to talk about the different cases based on the sibling node of this “double black” node

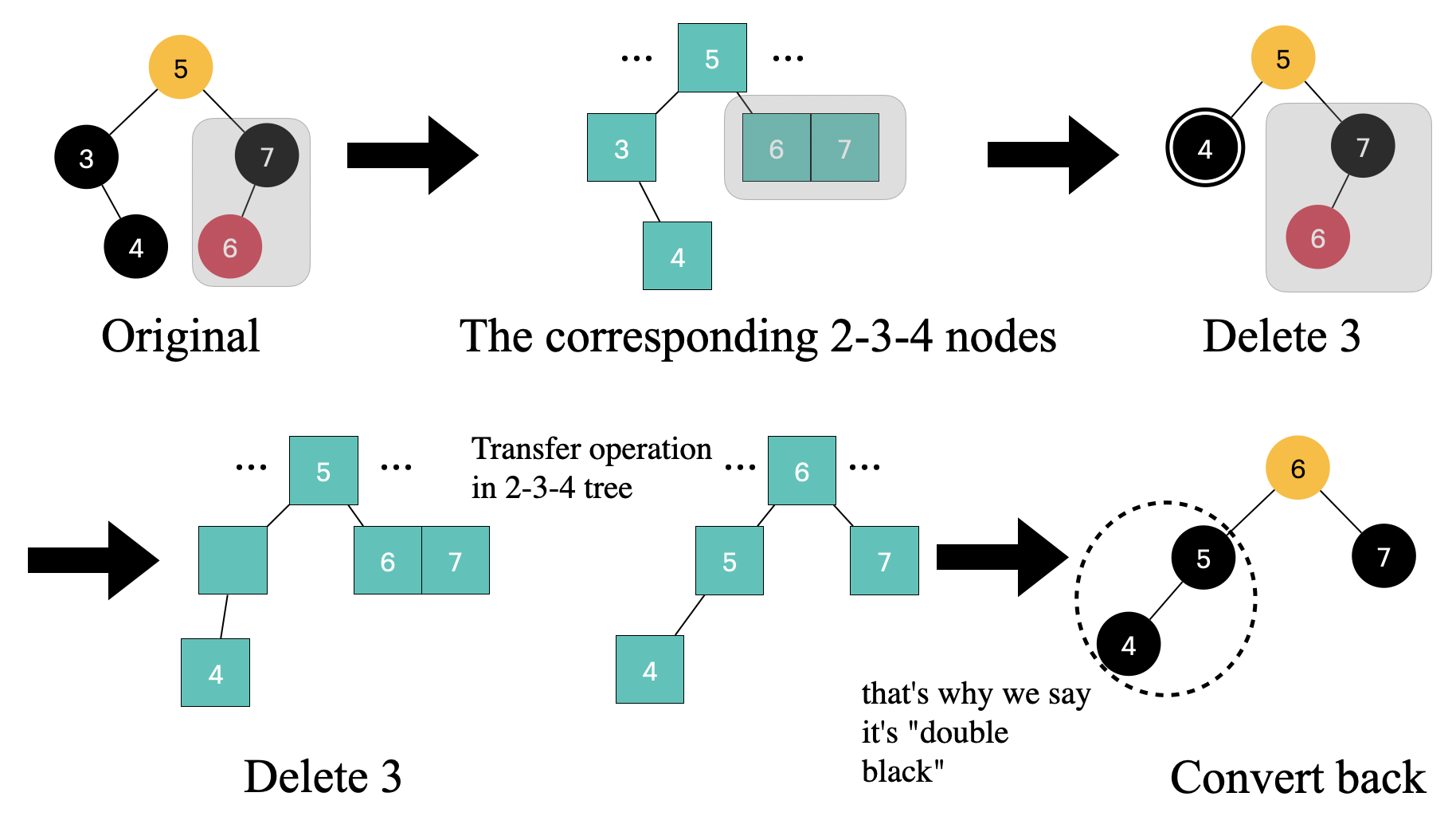
In the above example, when we transform it into an equivalent 2-3-4 tree deletion operation, we encounter a situation in the 2-3-4 tree where a transfer operation is required because the sibling nodes 6, 7 is a 3-node, and we need to borrow a key from them. The transfer operation involves moving the key from the parent node to the position of the deleted node, and then moving the minimum key from the sibling node to the parent node to fill the gap

💡 Note that now 4 and 5 are two black nodes. Previously, this was a special “double black” node, but now that we have two black nodes, the “double black” node is no longer necessary. That’s also the reason why it’s called a “double black” node—we need to remind ourselves that two black nodes are needed here.

💡 Note that the color of node 6 is the same as the original color of node 5

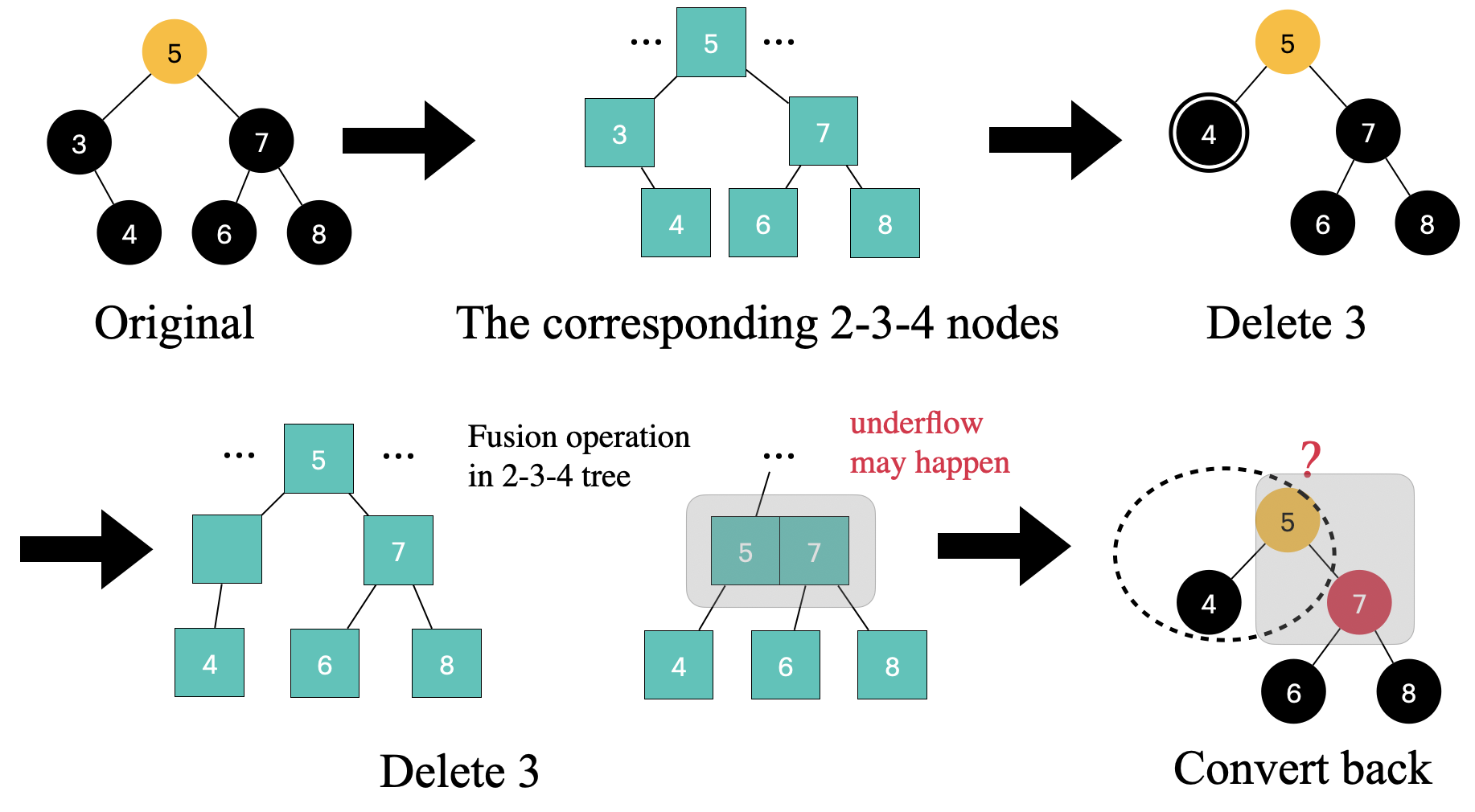
In the above example, when we transform it into an equivalent 2-3-4 tree deletion operation, we encounter a situation in the 2-3-4 tree where a fusion operation is required because the sibling node 7 is a 2-node and cannot lend a key. The fusion operation involves borrowing a key from the parent node and merging it with the sibling node to form a 3-node - 5, 7

💡 However, note that in this fusion operation, when we borrow a key from the parent node, it may cause the parent node to underflow, just as we may encounter overflow when inserting a new node.

Based on the node mappings rules, node 5 in this example should be colored black, and we can get rid of the “double black” node. However, we should not forget that 5 itself has its own color

  • If 5 was originally red, then changing it to black is not a problem because node 7 is now red
  • If 5 was originally black, then changing it to black would be problematic as it would result in a missing black node. In this case, node 5 becomes a new “double black” node, and we may need to continue adjusting upwards. This corresponds precisely to the underflow situation in a 2-3-4 tree. We need to bottom-up adjust our way back to the root node. Finally, if we find that the root node is a double black node, we simply change it to a black node.

The last scenario is when the sibling node is red and has two black children

💡 Note that if the sibling node is red, then the parent should be a black node, as a Red-black tree does not allow two consecutive red nodes

This situation can be cleverly transformed into one of the previous cases

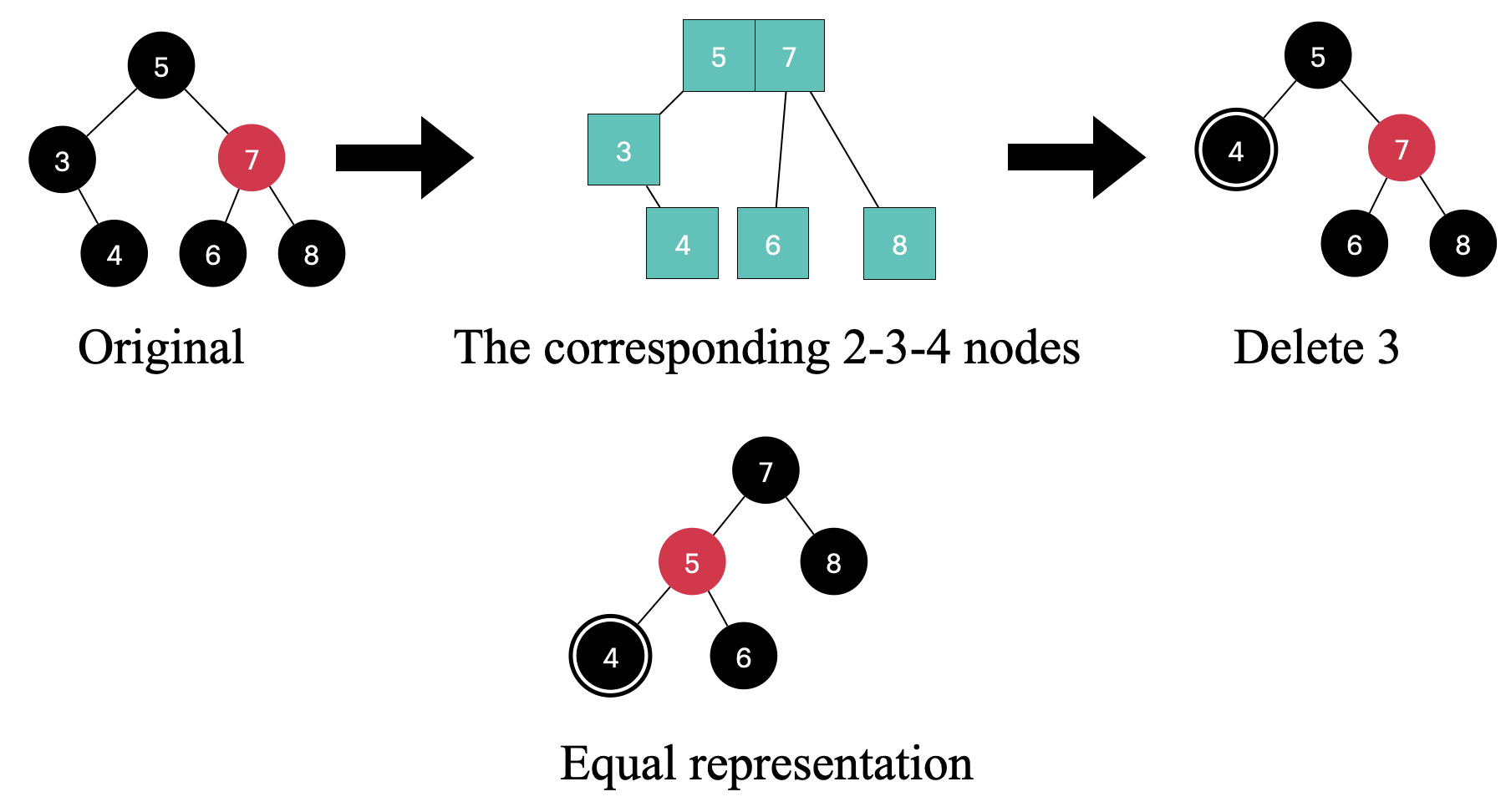
Now the node 4’s sibling node is black

After examining the previous examples, we have discovered that we can think about how to handle operations on a 2-3-4 tree and then convert it back to a Red-black tree. The operations of inserting and deleting nodes in a 2-3-4 tree are relatively simple, which is the main advantage of this approach. Most importantly, we no longer need to remember the rotation order and color exchanges, which is a significant improvement👏. That’s how I memorize the Red-black trees

  1. CS166. Balanced Trees, Part II ↩︎

  2. Red Black Trees ↩︎

Updated on 2023-07-01
 Data-Structure
 | Home