Posts Tags Categories

Hw06 - CS61A of UCB(2021-Fall)

MartinLwx  included in  category Course
     1509 words  8 minutes 

In this question you’ll create a vending machine that only outputs a single product and provides change when needed.

Create a class called VendingMachine that represents a vending machine for some product. A Vending Machineobject returns strings describing its interactions. Remember to match exactly the strings in the doctests – including punctuation and spacing!

Fill in the VendingMachine class, adding attributes and methods as appropriate, such that its behavior matches the following doctests:

According to the wiki, a vending machine is an automated machine that provides items to consumers after cash, or other forms of payment are inserted into the machine or otherwise made. To make this problem easier, the description indicates that the vending machine only has one product. Take care of the details:

  1. restock. The simplest function in Q1.
  2. add_funds
    1. Memorize the fund you add if it has stocks.
    2. Refund if there are no stocks at all
  3. vend
    1. Stocks available
      1. You can buy it if you have enough 💰
      2. It asks you to add more funds if your funds is not enough
      3. Don’t forget to decrease the stocks after you get the product.
    2. No stocks
      1. Restocks!

python

class VendingMachine:
    """A vending machine that vends some product for some price.
    """
    def __init__(self, product, price):
        self.product = product
        self.price = price
        self.balance = 0
        self.stocks = 0

    def restock(self, num):
        """Restock num items to our vending machine"""
        self.stocks += num
        return f"Current {self.product} stock: {self.stocks}"
    
    def add_funds(self, fund):
        """Add funds to balance, return funds if no stocks"""
        if self.stocks != 0:
            self.balance += fund
            return f"Current balance: ${self.balance}"
        else:
            return f"Nothing left to vend. Please restock. Here is your ${fund}."

    def vend(self):
        """Vend a product"""
        if self.stocks == 0:
            return 'Nothing left to vend. Please restock.'
        else:
            if self.balance < self.price:
                return f"You must add ${self.price - self.balance} more funds."
            else:
                change = self.balance - self.price
                self.balance = 0
                self.stocks -= 1
                if change == 0:
                    return f"Here is your {self.product}."
                else:
                    return f"Here is your {self.product} and ${change} change."

A mint is a place where coins are made. In this question, you’ll implement a Mint class that can output a Coin with the correct year and worth.

  • Each Mint instance has a year stamp. The update method sets the year stamp to the present_year class attribute of the Mint class.
  • The create method takes a subclass of Coin and returns an instance of that class stamped with the mint’s year (which may be different from Mint.present_year if it has not been updated.)
  • A Coin’s worth method returns the cents value of the coin plus one extra cent for each year of age beyond 50. A coin’s age can be determined by subtracting the coin’s year from the present_year class attribute of the Mint class.

:)

python

class Mint:
    """A mint creates coins by stamping on years.
    """
    present_year = 2021

    def __init__(self):
        self.update()

    def create(self, kind):
        return kind(self.year)

    def update(self):
        self.year = Mint.present_year


class Coin:
    def __init__(self, year):
        self.year = year

    def worth(self):
        age = Mint.present_year - self.year
        if age > 50:
            return self.cents + (age - 50) 
        else:
            return self.cents

Write a function store_digits that takes in an integer n and returns a linked list where each element of the list is a digit of n.

Important: Do not use any string manipulation functions like str and reversed

We can solve this problem iteratively. By calculating n % 10, we can get the last digit of the number, then we make a new node and insert it to the front of the linked list.

python

def store_digits(n):
    """Stores the digits of a positive number n in a linked list.
    """
    sentinel = Link(0)
    while n > 0:
        all_but_last, last = n // 10, n % 10
        # every time we insert node in the front of the linklist
        new_node = Link(n % 10, sentinel.rest)
        sentinel.rest = new_node
        n = all_but_last
    return sentinel.rest

Implement deep_map_mut(fn, link), which applies a function fn onto all elements in the given linked list link. If an element is itself a linked list, apply fn to each of its elements, and so on.

Your implementation should mutate the original linked list. Do not create any new linked lists.

Hint: The built-in isinstance function may be useful.

text

>>> s = Link(1, Link(2, Link(3, Link(4))))
>>> isinstance(s, Link)
True
>>> isinstance(s, int)
False

It is a recursive problem that needs to be solved recursively 🤗. Check the comments below.

python

def deep_map_mut(fn, link):
    """Mutates a deep link by replacing each item found with the
    result of calling fn on the item.  Does NOT create new Links (so
    no use of Link's constructor)
    """
    # base case 1. do thing if it is empty
    if link is Link.empty:
        return 
    # base case 2. if it is an integer
    if isinstance(link, int):
        link = fn(link)

    if isinstance(link.first, int):
        link.first = fn(link.first)
    else:
        deep_map_mut(fn, link.first)
    deep_map_mut(fn, link.rest)

Implement a function two_list that takes in two lists and returns a linked list. The first list contains the values that we want to put in the linked list, and the second list contains the number of each corresponding value. Assume both lists are the same size and have a length of 1 or greater. Assume all elements in the second list are greater than 0.

Unlike the previous problem(Q3), we insert the new node after the last node of the linked list.

python

def two_list(vals, amounts):
    """
    Returns a linked list according to the two lists that were passed in. Assume
    vals and amounts are the same size. Elements in vals represent the value, and the
    corresponding element in amounts represents the number of this value desired in the
    final linked list. Assume all elements in amounts are greater than 0. Assume both
    lists have at least one element.
    """
    idx = 0
    sentinel = Link(0)
    pos = sentinel
    while idx < len(vals):
        val, amount = vals[idx], amounts[idx]
        for _ in range(amount):
            new_node = Link(val)
            pos.rest = new_node
            pos = pos.rest
        idx += 1
    return sentinel.rest

Implement the next method of the VirFib class. For this class, the value attribute is a Fibonacci number. The next method returns a VirFib instance whose value is the next Fibonacci number. The next method should take only constant time.

Note that in the doctests, nothing is being printed out. Rather, each call to .next() returns a VirFib instance. The way each VirFib instance is displayed is determined by the return value of its __repr__ method.

Hint: Keep track of the previous number by setting a new instance attribute inside next. You can create new instance attributes for objects at any point, even outside the __init__ method.

:)

python

class VirFib():
    """A Virahanka Fibonacci number.
    """
    def __init__(self, value=0):
        self.value = value
        self.prev = 1

    def next(self):
        new_value = self.value + self.prev
        next_fin = VirFib(new_value)
        next_fin.prev = self.value
        return next_fin

    def __repr__(self):
        return "VirFib object, value " + str(self.value)

Write a function is_bst, which takes a Tree t and returns True if, and only if, t is a valid binary search tree, which means that:

  • Each node has at most two children (a leaf is automatically a valid binary search tree)
  • The children are valid binary search trees
  • For every node, the entries in that node’s left child are less than or equal to the label of the node
  • For every node, the entries in that node’s right child are greater than the label of the node

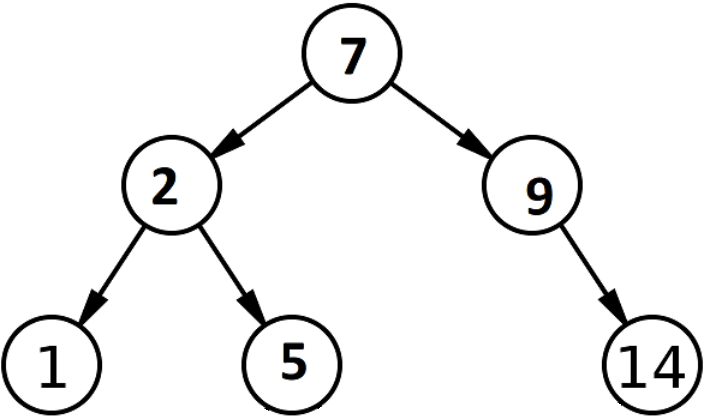
An example of a BST is:

bst

Note that, if a node has only one child, that child could be considered either the left or right child. You should take this into consideration.

Hint: It may be helpful to write helper functions bst_min and bst_max that return the minimum and maximum, respectively, of a Tree if it is a valid binary search tree.

Notable details:

  1. the minimal value of the left child should be <= the value of the current node rather than <.
  2. If a node has only one child, it can be considered either the left or right child.

python

def is_bst(t):
    """Returns True if the Tree t has the structure of a valid BST.
    """
    def bst_min(t):
        """Return the min value of the tree t"""
        if t.is_leaf():
            return t.label
        sub_branch_min = min([bst_min(b) for b in t.branches])
        return min(t.label, sub_branch_min)

    def bst_max(t):
        """Return the max value of the tree t"""
        if t.is_leaf():
            return t.label
        sub_branch_max = max([bst_max(b) for b in t.branches])
        return max(t.label, sub_branch_max)

    # base case 1. a leaf node is a BST
    if t.is_leaf():
        return True
    # base case 2. each node has at most 2 children
    if len(t.branches) > 2:
        return False
    # base case 3. a node with a single child
    # it can be considered either the left or the right
    if len(t.branches) == 1:
        return (bst_max(t.branches[0]) < t.label or bst_min(t.branches[0]) > t.label) \
                and is_bst(t.branches[0])

    left_max = bst_max(t.branches[0])
    right_min = bst_min(t.branches[1])
    return left_max <= t.label < right_min and is_bst(t.branches[0]) and is_bst(t.branches[1])
Updated on 2022-02-27
 Course, Python
 | Home