Lab04 solutions (UCB CS61A@2021 Fall)
Intro
I find it really interesting to solve recursive problems. I like this way of solving problems, the code is concise and intuitive, which is why I wrote this blog.
📒 How to solve a recursive problem ?
- What is the base case ?
- How to break down the current problem into simpler ones ?
Later, I will follow this idea to solve the recursion problem in this lab.
Recursion
Q2: Summation
Write a recursive implementation of
summation, which takes a positive integernand a functionterm. It appliestermto every number from1tonincludingnand returns the sum.Important: Use recursion; the tests will fail if you use any loops (for, while).
-
What is the base case ? This is easy to think, because we have to calculate from
1ton. Apparently,n = 1is the base case, which returnsterm(n) -
How to break down the current problem into simpler ones ? We call
summation(n - 1)to make this problem simpler.
def summation(n, term):
"""Return the sum of numbers 1 through n (including n) wíth term applied to each number.
Implement using recursion!
>>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
225
>>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
54
>>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
62
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(HW_SOURCE_FILE, 'summation',
... ['While', 'For'])
True
"""
assert n >= 1
# base case: n = 1
if n == 1:
return term(n)
else:
return term(n) + summation(n - 1, term)Tree Recursion
Q3: Pascal’s Triangle
Here’s a part of the Pascal’s trangle:
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1Every number in Pascal’s triangle is defined as the sum of the item above it and the item above and to the left of it. Use
0if the item does not exist.Define the procedure
pascal(row, column)which takes a row and a column, and finds the value of the item at that position in Pascal’s triangle. Rows and columns are zero-indexed; that is, the first row is row 0 instead of 1 and the first column is column 0 instead of column 1.For example, the item at row 2, column 1 in Pascal’s triangle is 2.
This probelm is a classical Problem. According to the definition, we know Pascal(i, j) = Pascal(i - 1, j) + Pascal(i - 1, j - 1). Apparently, the definition gives us a way to make this recursive problem easier. Then we have to ask us what is the base case ? By looking closely at Pascal’s triangle above, we will find it is always 1 when j = 0 and i == j.
Remember that we have to take care of empty entry. 🤔
def pascal(row, column):
"""returns the value of the item in pascal's triangle
whose position is specified by row and column.
>>> pascal(0, 0)
1
>>> pascal(0, 5) # empty entry; outside of pascal's triangle
0
>>> pascal(3, 2) # row 3 (1 3 3 1), column 2
3
>>> pascal(4, 2) # row 4 (1 4 6 4 1), column 2
6
"""
# in pascal's triangle, \
# pascal(i, j) = pascal(i - 1, j - 1) + pascal(i - 1, j)
# base case 1. empty entry
if column > row:
return 0
# base case 2. pascal(i, 0)
if column == 0:
return 1
# base case 3. pascal(i, i)
elif row == column:
return 1
return pascal(row - 1, column) + pascal(row - 1, column - 1)Q4: Insect Combinatorics
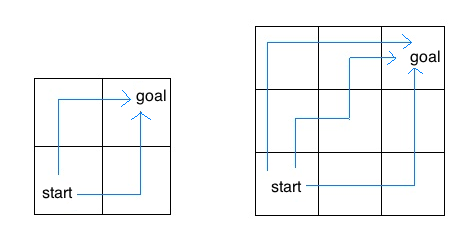
Consider an insect in an M by N grid. The insect starts at the bottom left corner, (0, 0), and wants to end up at the top right corner, (M-1, N-1). The insect is only capable of moving right or up. Write a function
pathsthat takes a grid length and width and returns the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).
Hint: What happens if we hit the top or rightmost edge?
From the description, we know that we can only move right or up. Suppose we are in paths(i, j), we know we can only come from the left or the bottom. So we can draw a conclusion: path(i, j - 1) + path(i - 1, j). (the bottom left = (0, 0)). Then, what is the base case ?」, see the table below:
| 1 | ||
|---|---|---|
| 1 | ||
| 1 | 1 | 1 |
According to the above formula, we can know that the complete table should be like this:
| 1 | 3 | 6 |
|---|---|---|
| 1 | 2 | 3 |
| 1 | 1 | 1 |
To make this problem easier, we let the index start at 1 🤗
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
# base case path(i, 0) or path(0, i)
if m == 1 or n == 1:
return 1
return paths(m, n - 1) + paths(m - 1, n)List Comprehensions
Q5: Couple
Implement the function
couple, which takes in two lists and returns a list that contains lists with i-th elements of two sequences coupled together. You can assume the lengths of two sequences are the same. Try using a list comprehension.Hint: You may find the built in range function helpful.
This is a simple question, because the two lists are the same length. We just need to use the same index to fetch numbers from the two lists.
def couple(s, t):
"""Return a list of two-element lists in which the i-th element is [s[i], t[i]].
>>> a = [1, 2, 3]
>>> b = [4, 5, 6]
>>> couple(a, b)
[[1, 4], [2, 5], [3, 6]]
>>> c = ['c', 6]
>>> d = ['s', '1']
>>> couple(c, d)
[['c', 's'], [6, '1']]
"""
assert len(s) == len(t)
return [[s[i], t[i]] for i in range(len(s))]Q6: Coordinates
Implement a function
coordsthat takes a functionfn, a sequenceseq, and alowerandupperbound on the output of the function.coordsthen returns a list of coordinate pairs (lists) such that:
- Each (x, y) pair is represented as
[x, fn(x)]- The x-coordinates are elements in the sequence
- The result contains only pairs whose y-coordinate is within the upper and lower bounds (inclusive)
See the doctest for examples.
Note: your answer can only be one line long. You should make use of list comprehensions!
We need to add an if statement to filter out the results that do not meet the conditions.
def coords(fn, seq, lower, upper):
"""
>>> seq = [-4, -2, 0, 1, 3]
>>> fn = lambda x: x**2
>>> coords(fn, seq, 1, 9)
[[-2, 4], [1, 1], [3, 9]]
"""
"*** YOUR CODE HERE ***"
return [[i, fn(i)] for i in seq if lower <= fn(i) <= upper]Q7: Riffle Shuffle
A common way of shuffling cards is known as the riffle shuffle. The shuffle produces a new configuration of cards in which the top card is followed by the middle card, then by the second card, then the card after the middle, and so forth.
Write a list comprehension that riffle shuffles a sequence of items. You can assume the sequence contains an even number of items.
Hint: There are two ways you can write this as a single list comprension: 1) You may find the expression
k%2, which evaluates to 0 on even numbers and 1 on odd numbers, to be alternatively access the beginning and middle of the deck. 2) You can utilize an if expression in your comprehension for the odd and even numbers respectively.
This problem will be a little more difficult. We are actually trying to find a way to get the correct index in List Comprehensions. Obviously, the situation is different when the index is odd and even. We can look at the following table to guess the rules⬇️:
| Origin index | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Real index for deck[…] | 0 | 2 | 1 | 3 |
| Guess ? (M = 2) | 0 | M | 2 // 2 ? | M + 1 = M + 3 // 2 ? |
- odd: 0, 1, 2, … ->
i // 2 - even: M+0, M+1, M+2, … ->
M + i // 2
def riffle(deck):
"""Produces a single, perfect riffle shuffle of DECK, consisting of
DECK[0], DECK[M], DECK[1], DECK[M+1], ... where M is position of the
second half of the deck. Assume that len(DECK) is even.
>>> riffle([3, 4, 5, 6])
[3, 5, 4, 6]
>>> riffle(range(20))
[0, 10, 1, 11, 2, 12, 3, 13, 4, 14, 5, 15, 6, 16, 7, 17, 8, 18, 9, 19]
"""
return [deck[i // 2 + (i % 2) * (len(deck) // 2)] for i in range(len(deck))]