Lab10 solutions (UCB CS61A@2021 Fall)

Coding Questions

Q2: Over or Under

Define a procedure over-or-under which takes in a number num1 and a number num2 and returns the following:

• -1 if num1 is less than num2
• 0 if num1 is equal to num2
• 1 if num1 is greater than num2

Challenge: Implement this in 2 different ways using if and cond!

text

(define (over-or-under num1 num2)
  'YOUR-CODE-HERE
)

The problem itself is not difficult. We just need to get used to the grammar of the scheme language. If we want to indicate the conditional branches, we may use:

1. (if <predicate> <consequent> <alternative>)
2. (cond (<condition> <consequent>) ...)

(define (over-or-under num1 num2) 
    (if (< num1 num2) 
            (print -1))
    (if (= num1 num2)
            (print 0))
    (if (> num1 num2)
            (print 1))
)

(define (over-or-under num1 num2)
  (cond ( (< num1 num2) (print -1) )
        ( (= num1 num2) (print 0)  )
        ( (> num1 num2) (print 1)  ))
)

Q3: Make Adder

Write the procedure make-adder which takes in an initial number, num, and then returns a procedure. This returned procedure takes in a number inc and returns the result of num + inc.

Hint: To return a procedure, you can either return a lambda expression or define another nested procedure. Remember that Scheme will automatically return the last clause in your procedure.

You can find documentation on the syntax of lambda expressions in the 61A scheme specification!

We once saw make-adder written in python in the course. Now we have to translate it to the scheme language. I will use the lambda function to implement the high-order function.

(define (make-adder num)
  (lambda (inc) (+ num inc))
)

Q4: Compose

Write the procedure composed, which takes in procedures f and g and outputs a new procedure. This new procedure takes in a number x and outputs the result of calling f on g of x.

Is is similar to Q3.

(define (composed f g)
  (lambda (x) (f (g x) ) )
)

Q5: Make a List

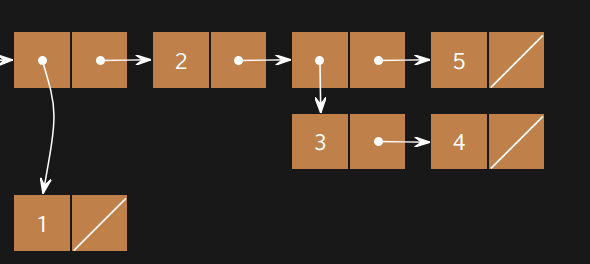
In this problem you will create the list with the following box-and-pointer diagram:

Challenge: try to create this list in multiple ways, and using multiple list constructors!要求

This problem asks us to make a list depending on the structure provided. We can implement this in many different ways:

1. cons, the basic way to define a list in scheme. I felt a little dizzy after finishing this 😢
2. list, the code is shorter. Notice that every time we call (list ...), it is equivalent to making a sublist in the list(a new direction)

(define lst 
  (cons (cons 1 nil)
        (cons 2 (cons (cons 3 (cons 4 nil))
                      (cons 5 nil))))
)

(define lst 
  (list (list 1)
        2 (list 3 4)
        5)
)

Optional Questions

Q6: Remove

Implement a procedure remove that takes in a list and returns a new list with all instances of item removed from lst. You may assume the list will only consist of numbers and will not have nested lists.

Hint: You might find the built-in filter procedure useful (though it is definitely possible to complete this question without it).

You can find information about how to use filter in the 61A Scheme builtin specification!

In face, the list of the scheme language is a linklist. So the problem is removing elements whose value are equal to item. Apparently, We can solve this problem recursively. The assumption that there are no nested lists in Q6 makes the problem easier.

The base case is a empty list, we will return '(). Otherwise,

1. The value of current node = item, exclude it and process sublist recursively.
2. The value of current node != item, include it and process sublist recursively.

(define (remove item lst)
  (cond ( (null? lst) '() )             ; base case
        ( (= item (car lst)) (remove item (cdr lst)))           ; exclude item
        ( else (cons (car lst) (remove item (cdr lst)))))       ; include item
)