LoRA fine-tuning
What’s LoRA
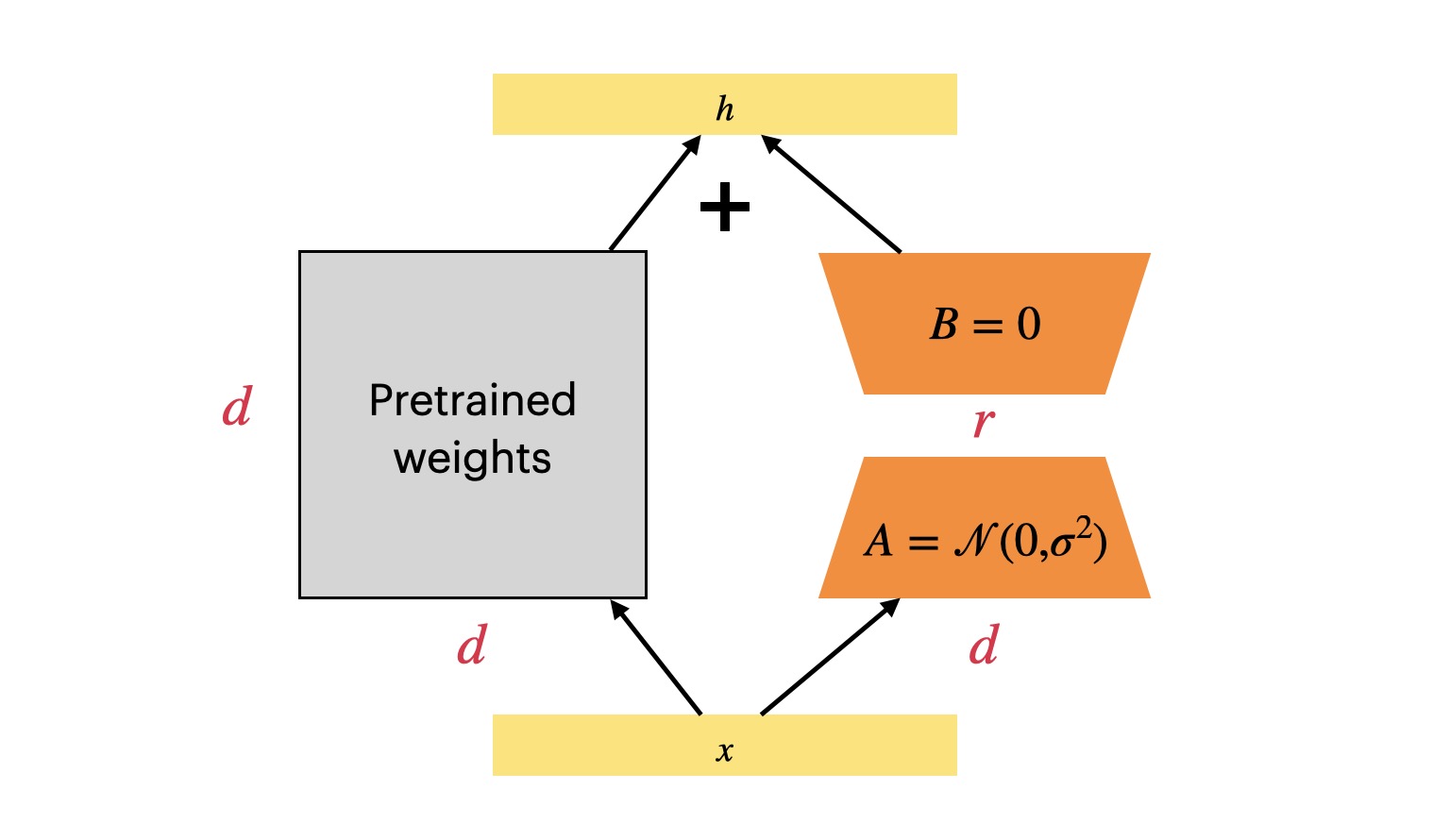
Since the era of LLM(large language model) arrived, fine-tuning LLM has become a challenge because the LLM models are extremely large, making it difficult to perform full fine-tuning. There are mainly two approaches: freeze the entire LLM and perform prompt tuning or In-context Learning; freeze the entire LLM but inserting trainable modules. Today, I will introduce the LoRA(Low-Rank Adaptation), which corresponds to the latter technical approach. This is a work proposed by the Microsoft team1
The idea behind LoRA is quite simple. If you are familiar with deep learning, you should know that the parameters are updated by the gradient descent. Let’s consider a weight matrix $\mathbf W_0\in\mathcal{R}^{d\times d}$(the subscript 0 here means it’s the initial value), we can use $\Delta \mathbf W$ to denote the relative change to the initial value when it has been trained. After training, the parameters of this matrix will be
$$\mathbf W_0+\Delta \mathbf W$$
The problem that LoRA aims to solve is whether it is possible to determine the $\Delta \mathbf W$ without altering $\mathbf W_0$ and with minimal computation cost. This is achievable because researchers have found that the intrinsic rank of a learned LLM model is low. Therefore, the authors hypothesize that the weight change($\Delta \mathbf W$) during model adaption also has a low intrinsic rank, which allows us to perform a low-rank decomposition of $\Delta\mathbf W$. Experimental results have shown that this assumption holds, and LoRA fine-tuning achieves promising results1. The low-rank decomposition is as follows
$$\Delta \mathbf W=\mathbf B\mathbf A$$
where $\mathbf B\in\mathcal{R}^{d\times r}$,$\mathbf A\in\mathcal{R}^{r\times d}$, the matrix $\mathbf B$ is initialized with zero and the matrix $\mathbf A$ is initialized with a random Gaussian. This ensures that at the beginning of training, the LoRA module has no impact on the original model.
If the input is $\mathbf x$, then the computation will be
$$\mathbf W_0\mathbf x+\frac{\alpha}{r}\Delta \mathbf W\mathbf x=\mathbf W_0\mathbf x+\frac{\alpha}{r}\mathbf B\mathbf A\mathbf x$$
The $\alpha$ here is a scaling factor, and $r$ is the value of low-rank
During training, only $\mathbf B$ and $\mathbf A$ are updated by the gradient descent. During inference, we can combine $\mathbf W_0$ with $\mathbf B\mathbf A$ just like the LoRA module does not exist. It is a significant advantage of LoRA: it does not introduce inference latency👍
Additionally, we can calculate the change in the number of learnable parameters when using LoRA.
$$ (\mathbf W_0+\frac{\alpha}{r}\Delta\mathbf W)\mathbf x=\mathbf W_0\mathbf x+\frac{\alpha}{r}\Delta \mathbf W\mathbf x=\mathbf W_0\mathbf x+\frac{\alpha}{r}\mathbf B\mathbf A\mathbf x $$
The learnable parameters we need to train are significantly reduced because $r\ll d$, which makes LoRA a parameter-efficient fine-tuning method. 👍
Two questions remaining - where should LoRA be applied in the transformer architecture? what is the optimal value for r?
- In section 7.1 of the paper, the authors found that applying LoRA to both the $\mathbf W_q$ and $\mathbf W_v$ yields the best result1
- In section 7.2 of the paper, the authors discovered that increasing
rdoes not always lead to significant improvements. and the values around4 ~ 8work well, which suggest that a low-rank adaptation matrix is sufficient1
How to use LoRA
The Huggingface has a library called peft which supports LoRA fine-tuning and many other fine-tuning techniques. The README.md file in this repo explains how to use LoRA fine-tuning. We simply need to configure the parameters using LoraConfig, and then use get_peft_model to transform the model, making it ready for subsequent training.
from transformers import AutoModelForCausalLM
from peft import get_peft_config, get_peft_model, LoraConfig, TaskType
model_name_or_path = "facebook/opt-350m"
peft_config = LoraConfig(
task_type=TaskType.CAUSAL_LM,
r=8,
lora_alpha=32,
lora_dropout=0.1,
)
model = AutoModelForCausalLM.from_pretrained(model_name_or_path)
model = get_peft_model(model, peft_config)
model.print_trainable_parameters()
# output: trainable params: 786,432
# || all params: 331,982,848
# || trainable%: 0.2368893467652883After training, we can save the model by using model.save_pretrained(output_dir), where output_dir means the path to save. If we check the output_dir folder, you will find that we only saved the incremental PEFT weights rather than the whole model weights
output_dir
├── README.md
├── adapter_config.json
└── adapter_model.binTo load the model and the LoRA module, we can leverage this magic API :)
from peft import AutoPeftModelForCausalLM
peft_model_name_or_path = "./output_dir"
model = AutoPeftModelForCausalLM.from_pretrained(peft_model_name_or_path)The source code of LoRA
I omit some irrelevant parts of the source code for brevity. The code below is from the
peft 0.5.0
The core of the LoRA fine-tuning implementation is the LoraModel class
class LoraModel(BaseTuner):
def __init__(self, model, config, adapter_name) -> None:
super().__init__(model, config, adapter_name)
...It can be seen from the code that LoraModel inherits from the BaseTuner class, and it just calls the constructor of BaseTuner
class BaseTuner(nn.Module, ABC):
def __init__(self, model, peft_config, adapter_name) -> None:
super().__init__()
self.model = model
self.inject_adapter(self.model, adapter_name)
self.model.peft_config = self.peft_configLet’s focus on the inject_adapter method
class BaseTuner(nn.Module, ABC):
def inject_adapter(self, model: nn.Module, adapter_name: str):
peft_config = self.peft_config[adapter_name]
is_target_modules_in_base_model = False
key_list = [key for key, _ in model.named_modules()]
peft_config = self._prepare_adapter_config(peft_config, model_config)
for key in key_list:
if not self._check_target_module_exists(peft_config, key):
continue
is_target_modules_in_base_model = True
parent, target, target_name = _get_submodules(model, key)
optionnal_kwargs = {
"loaded_in_8bit": getattr(model, "is_loaded_in_8bit", False),
"loaded_in_4bit": getattr(model, "is_loaded_in_4bit", False),
"current_key": key,
}
self._create_and_replace(
peft_config,
adapter_name,
target,
target_name,
parent,
**optionnal_kwargs,
)
self._mark_only_adapters_as_trainable()
if self.peft_config[adapter_name].inference_mode:
for n, p in self.model.named_parameters():
if adapter_name in n:
p.requires_grad = FalseThe inject_adapter just iterates all modules and checks which one we want to modify by the name of the module. The key here is the _create_and_replace method
class LoraModel(BaseTuner):
def _create_and_replace(
self,
lora_config,
adapter_name,
target,
target_name,
parent,
**optionnal_kwargs,
):
bias = hasattr(target, "bias") and target.bias is not None
kwargs = {
"r": lora_config.r,
"lora_alpha": lora_config.lora_alpha,
"lora_dropout": lora_config.lora_dropout,
"fan_in_fan_out": lora_config.fan_in_fan_out,
"init_lora_weights": lora_config.init_lora_weights,
}
kwargs["loaded_in_8bit"] = optionnal_kwargs.pop("loaded_in_8bit", False)
kwargs["loaded_in_4bit"] = optionnal_kwargs.pop("loaded_in_4bit", False)
kwargs["bias"] = bias
if isinstance(target, LoraLayer) and isinstance(target, torch.nn.Conv2d):
...
else:
new_module = self._create_new_module(
lora_config, adapter_name, target, **kwargs
)
self._replace_module(parent, target_name, new_module, target)We are interested in how LoRA changes the nn.Linear module, so we should dive into the _create_new_module method
class LoraModel(BaseTuner):
def _create_new_module(lora_config, adapter_name, target, **kwargs):
if loaded_in_8bit and isinstance(target, bnb.nn.Linear8bitLt):
...
else:
if isinstance(target, torch.nn.Linear):
in_features, out_features = target.in_features, target.out_features
elif isinstance(target, Conv1D):
...
else:
...
new_module = Linear(
adapter_name,
in_features,
out_features,
bias=bias,
**kwargs
)
return new_moduleFirst, we copy the in_features and out_features attributes of the nn.Linear module, and then we create a new Linear module. We can find the Linear module definition in the same file
class Linear(nn.Linear, LoraLayer):
def __init__(
self,
adapter_name: str,
in_features: int,
out_features: int,
r: int = 0,
lora_alpha: int = 1,
lora_dropout: float = 0.0,
fan_in_fan_out: bool = False,
is_target_conv_1d_layer: bool = False,
**kwargs,
):
init_lora_weights = kwargs.pop("init_lora_weights", True)
nn.Linear.__init__(self, in_features, out_features, **kwargs)
LoraLayer.__init__(self, in_features=in_features, out_features=out_features)
# Freezing the pre-trained weight matrix
self.weight.requires_grad = False
nn.Linear.reset_parameters(self)
self.update_layer(adapter_name, r, lora_alpha, lora_dropout, init_lora_weights)
self.active_adapter = adapter_nameSo the Linear just calls the constructor of nn.Linear and LoraLayer. Note that the self.weight refers to the original weight which is frozen. The update_layer method will set the LoRA module
class LoraLayer(BaseTunerLayer):
def __init__(self, in_features: int, out_features: int, **kwargs):
self.r = {}
self.lora_alpha = {}
self.scaling = {}
self.lora_dropout = nn.ModuleDict({})
self.lora_A = nn.ModuleDict({})
self.lora_B = nn.ModuleDict({})
# For Embedding layer
self.lora_embedding_A = nn.ParameterDict({})
self.lora_embedding_B = nn.ParameterDict({})
# Mark the weight as unmerged
self.merged = False
self.disable_adapters = False
self.in_features = in_features
self.out_features = out_features
self.kwargs = kwargs
def update_layer(
self, adapter_name, r, lora_alpha, lora_dropout, init_lora_weights
):
self.r[adapter_name] = r
self.lora_alpha[adapter_name] = lora_alpha
if lora_dropout > 0.0:
lora_dropout_layer = nn.Dropout(p=lora_dropout)
else:
lora_dropout_layer = nn.Identity()
self.lora_dropout.update(nn.ModuleDict({adapter_name: lora_dropout_layer}))
# Actual trainable parameters
if r > 0:
self.lora_A.update(
nn.ModuleDict(
{adapter_name: nn.Linear(self.in_features, r, bias=False)}
)
)
self.lora_B.update(
nn.ModuleDict(
{adapter_name: nn.Linear(r, self.out_features, bias=False)}
)
)
self.scaling[adapter_name] = lora_alpha / r
if init_lora_weights:
self.reset_lora_parameters(adapter_name)
self.to(self.weight.device)Finally, we find where LoRA set up $\mathbf A$ and $\mathbf B$. We can also find the aforementioned scaling factors in this code. One question remaining - What does this module do in the forward pass?
class LoraLayer(BaseTunerLayer):
def forward(self, x: torch.Tensor):
previous_dtype = x.dtype
if self.disable_adapters:
...
elif self.r[self.active_adapter] > 0 and not self.merged:
result = F.linear(
x, transpose(self.weight, self.fan_in_fan_out), bias=self.bias
)
x = x.to(self.lora_A[self.active_adapter].weight.dtype)
result += (
self.lora_B[self.active_adapter](
self.lora_A[self.active_adapter](
self.lora_dropout[self.active_adapter](x)
)
)
* self.scaling[self.active_adapter]
)
else:
...
result = result.to(previous_dtype)
return resultLooking at the code, it becomes clear that the input x serves as the input for both the model’s original nn.Linear layer and the LoRA module. The LoRA module also performs scaling at the end, everything aligns with the explanation mentioned earlier