Reading Notes: REALM: Retrieval-Augmented Language Model Pre-Training
Introduction
Recently I was planning to learn the RAG technology so I started to read some related papers. I found a good Roadmap in the ACL 2023 Tutorial’s slide. Today’s topic is the most fundamental one: Retrieval-Augmented Language Model Pre-Training (REALM).
The REALM framework uses the Masked LM (BERT) rather than LLM. So I assume that you have a basic understanding of BERT such as how to do pre-train/fine-tuning.
The idea
Here is the motivation: The knowledge is stored in the model implicitly. The authors proposed the REALM framework and add a retriever. The job of the retriever is to retrieve relevant documents from a large corpus.
If you are familiar with BERT, you may recall that it can only handle 512 tokes at most. Therefore, the “a document” here actually refers to a text chunk.
The architecture is illustrated in the following diagram1
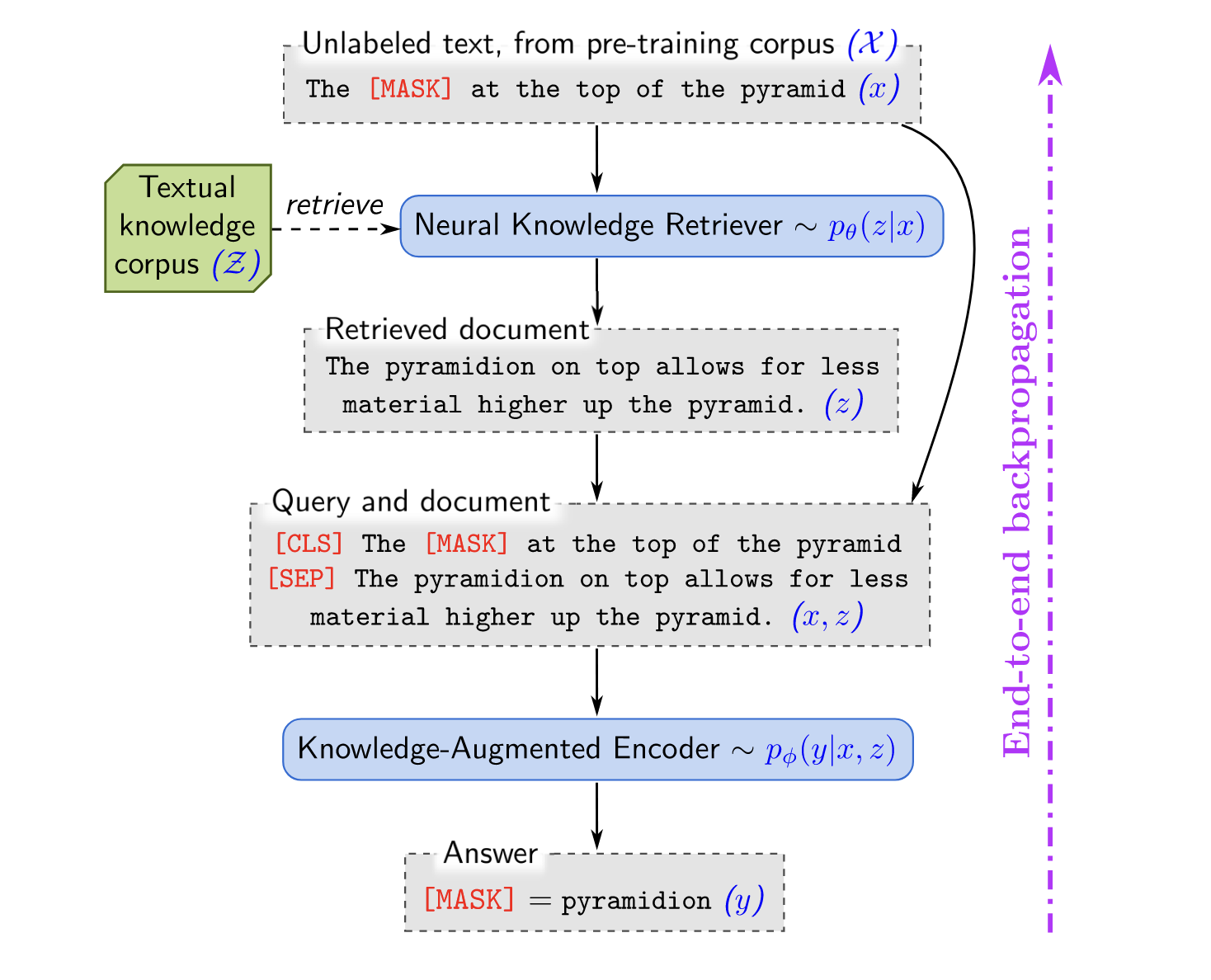
- The language model refers to BERT, so you can see the special tokens (
[CLS], [MASK], [SEP]) - The text chunk retrieved by the retriever is concatenated with the query using
[SEP]
Now that there is an additional retriever, several issues need to be addressed.
- How to train a retriever?
- The corpus (denoted as $\mathcal Z$ in the diagram) is very large. How to minimize the cost when retrieving? How to measure the relevance between text chunk and query? How to find the most relevant documents?
- How to use the retrieved text chunk?
For the first question, the author proposed a an unsupervised learning way that uses perplexity as a signal. If the output of the perplexity becomes smaller after you use the retrieved text chunk, then the retrieved text chunk is useful :)
For the second question, each document will be split into multiple text chunks. By using the BERT model, each text chunk can get its embedding. The relevance between the query and text chunk is defined as the inner product of the corresponding embeddings.
For the third question, the retrieved text chunk will just be concatenated with the query using [SEP]
The model architecture
Let’s denote the input as $x$, output as $y$ and retrieved text chunk as $z$. What we want to do is give input predicting the output, that is
$$ p(y|x) $$
The REALM framework calculates this equation in two stages
- retrieve: retrieve the text chunk $z$ from the corpus $\mathcal Z$. This procedure can be modeling with $p(z|x)$
- predict: given the input $x$ and the retrieved text chunk $z$ the model needs to generate output $y$, that is, $p(y|z,x)$
Retriever
Let’s look into the retriever first which handles $p(z|x)$
$$ \begin{aligned} p(z|x)&=\frac{exp\ f(x,z)}{\sum_{z’}exp\ f(x,z’)} \\ f(x,z)&=\texttt{Embed}_{input}(x)^T\texttt{Embed}_{doc}(z) \end{aligned} $$
The equations may be confusing in the first look. However, the idea is quite simple. Let me translate it into English: we need to calculate the embedding of the input ($\texttt{Embed}_{input}(x)$) and the embeddings of each text chunk $z$ ($\texttt{Embed}_{doc}(z)$) in corpus $\mathcal Z$, and then calculating the inner product. After the $\texttt{softmax}$ function ($\frac{exp\ …}{\sum exp…}$) we got a probability distribution $p(z|x)$, and then we know the relevance for each text chunk.
The procedure of using BERT to extract the embedding is easy to understand. The output embedding of the [CLS] token is considered as the representation of the input, and the author also performs a linear project to reduce the dimensionality. The key issue is what the input should be?
The author defines such templates.
$$ \begin{aligned} \texttt{join}_\texttt{BERT}(x)&=\texttt{[CLS]}x\texttt{[SEP]} \\ \texttt{join}_\texttt{BERT}(x_1,x_2)&=\texttt{[CLS]}x_1\texttt{[SEP]}x_2\texttt{[SEP]} \end{aligned} $$
- For the query, that is $\texttt{join}_\texttt{BERT}(query)$
- For the text chunk, that is $\texttt{join}_\texttt{BERT}(z_{title}, z_{body})$. The interesting thing is that the title and body are explicitly separated
Encoder
The calculation of $p(y|z,x)$ is addressed by the encoder. The author distinguishes between pre-train and fine-tuning scenarios. I won’t go into detail about these two cases because it is the age of LLM now. Let’s take a look at the input.
$$ \texttt{join}_{\texttt{BERT}}(x, z_{\texttt{body}}) $$
Training
We want to optimize the $p(y|x)$ distribution and it can be calculated by the marginal probability
$$ p(y|x)=\sum_{z\in\mathcal Z}p(y|z,x)p(z|x) $$
There are a few challenges here.
- The $\sum_{z\in\mathcal Z}$ part needs to do summation over all text chunks in $\mathcal Z$, which incurs particular high performance overhead. The author suggests that it can be approximated by summing over the top-k text chunks as the unrelated text chunk’s $p(z|x)\approx 0$
- Previously, I said that the embeddings of text chunks can be calculated in advance. However, if the parameters of model $\texttt{Embed}_{doc}$ get updated, the embeddings will stale. Ideally, the embedding of each text chunk should be updated after each model update, but this would impact training.
- pre-train: the model $\texttt{Embed}_{doc}$’s parameters will be updated after hundreds of steps (500 in the paper), and then the embeddings of each text chunk will be refreshed.
- fine-tuning: in fine-tuning setting, the model $\texttt{Embed}_{doc}$ is frozen, that is, the parameters won’t got updated at all.
Warp-up
The REALM framework proposed in 2020 is the RAG technology in the BERT model. Although the BERT model is less relevant in 2024, the design choices of the REALM framework have some aspects worth learning for
- The retrieving process can be done only once in the beginning.
- If the corpus is large, then we could focus on the top-k choices.