How KNN Algorithm Works

What’ is KNN Algorithm

The K nearest neighbors (KNN) algorithm allows us to determine the class of a new sample (denoted as $\mathbf x$) based on a set of samples with known classes. The principle of KNN is to consider the classes of the $K$ nearest neighbors to it

Then, there are several key issues worth investigating.

• What is the optimal $K$?
• How to measure distances between samples?
• How to aggregate the class results of the $K$ neighbors?

The value of K

The bigger the $K$ is, the more samples we need to consider. Thus, the classification result should be more accurate theoretically. However, If we consider too many samples, we may include the less related samples which would make the prediction less accurate.

If the $K$ is small, then the variance of KNN’s prediction will get higher.

Thus, the $K$ needs to be carefully chosen, in practice, you can gradually increase $K$, and monitor the performance on the validation set. By plotting a curve with $K$ on the x-axis and validation on the y-axis, the elbow point of the curve indicates the optimal $K$. This is known as the elbow method.

The optimal $K$ can also be calculated by the cross-validation method.

The distance measurement

Each sample is represented as a $d$-dimensional vector. A popular distance measurement is the Euclidean Distance.

$$ \texttt{distance}(\mathbf x,\mathbf y)=\sqrt{\sum_{i=1}^d(x_i-y_i)^2} $$

The aggregation of K neighbors’ results

After figuring out the $K$ nearest neighbors, the result is calculated by a plurality vote of its $K$ neighbors.

Implementation

The Scikit-Learn library provides us with API to create a KNN classifier. Before creating such a classifier, let’s generate our toy dataset first.

import numpy as np
np.random.seed(40)
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(
    n_samples=100,
    n_features=2,
    n_informative=2,
    n_redundant=0,
    n_clusters_per_class=1,
    random_state=40,
)
X_train, X_temp, y_train, y_temp = train_test_split(
    X, y, test_size=0.2, random_state=40
)

X_valid, X_test, y_valid, y_test = train_test_split(
    X_temp, y_temp, test_size=0.5, random_state=40
)

To get a better understanding of this toy dataset, I draw a scatter plot as follows.

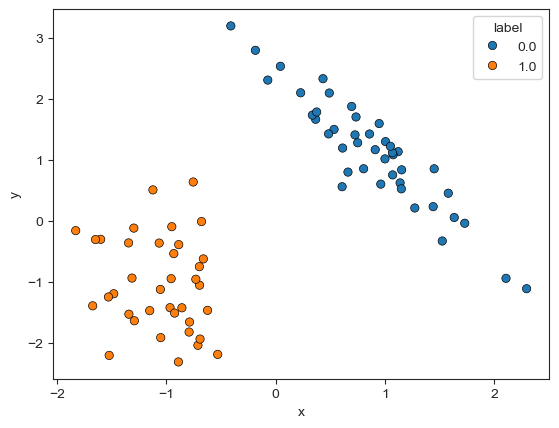
Now we can create a KNN classifier and “train” it on the training set X_train.

from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=5)
neigh.fit(X_train, y_train)

Now given a new sample represented as [0, 0], we can use the KNN classifier to get its class label.

test_point = [0, 0]
neigh.predict([test_point])
# array([1])

Let’s plot its 5 neighbors to figure out how KNN makes its decision. The black $\times$ symbol represents the neighbors, and the red $\times$ symbol is the new sample.

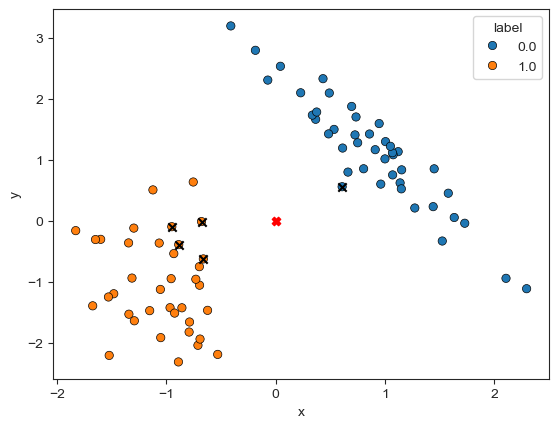
From this diagram, we find that 4 neighbors have class label 1 and 1 neighbor has class label 0, so the KNN classifier predicts [0, 0] has class label 1.

FAQ

Can we use KNN on the unbalanced dataset?

It’s not recommended to use KNN in cases of unbalanced dataset, as the algorithm will almost always classify new samples into the majority class

The value of K and the complexity of KNN

An interesting question is: what’s the relationship between the value of $K$ and the complexity of KNN?

The answer is that the smaller the $K$ is, the more complex the model becomes, making it more prone to overfitting.

Looking at it the other way around: when $K$ is at its maximum, equal to the total number of samples ($N$), any new samples will always be classified as the majority class in the dataset. This kind of model is obviously overly simplistic.

Should we normalize the sample vector?

Yes. Because the KNN relies on the distance measurement. If the feature vector comes in vastly different scales, the feature with larger numerical values will dominate the distance calculation.

Can we use KNN for regression problems?

Yes. In the classification settings, the KNN classifier uses a voting method to decide the class label. If we apply KNN to the regression problem, the prediction can be modeled as the weighted sum of $K$ neighbors’s value.

How can we improve the naive KNN algorithm?

A naive KNN algorithm uses voting to decide the class label of a new sample. In such a setting, each neighbor has the same contribution to the final prediction. One possible improvement may be to change the contribution of each label by its distance to a new sample. An intuition is: the closer a neighbor is, the more the neighbor contributes. A commonly used weighting schema is $1/d$ where $d$ is the distance to the new sample.