Reading Notes: Generalization through Memorization: Nearest Neighbor Language Models
Motivation
A language solves 2 subproblems.
- Mapping sentence prefixes to fixed-size representation.
- Using these representations to predict the next token in the context.
The $k\texttt{NN-LM}$ proposed in this hypothesis that representation learning problem may be easier than the prediction problem
kNN-LM
The following graph demonstrates the idea behind the $k\texttt{NN-LM}$ model.
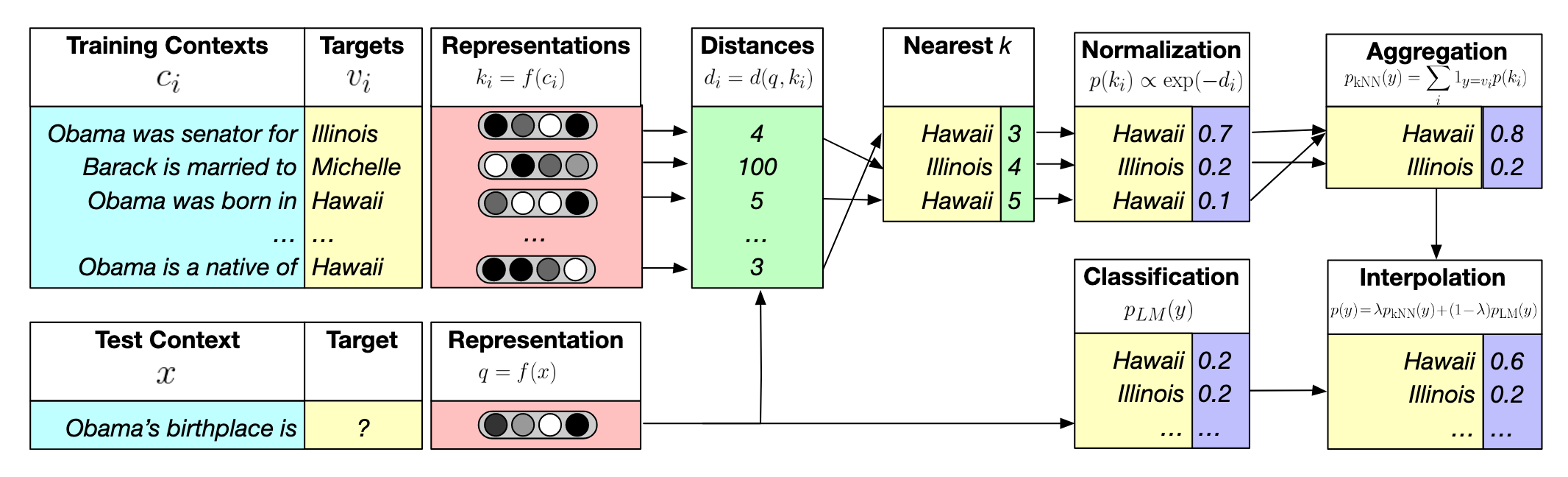
Data Preparation
To use the $k\texttt{NN-LM}$, we need to preprocess the documents in the corpus. The preprocessing procedure can be divided into some steps. Take the following sentence as an example.
Today is a good [day]This sentence can be broken into two parts.
Today is a good day: it’s referred to the context (denoted as $c_i$). If we use this as the LLM’s input, we can get the vector representation $f(c_i)$.day: it’s called target in this paper, which represents the next token $w_i$.
Now we have $(f(c_i),w_i)$ pair, which can be stored in a KV database (that is, datastore)
Inference
Previously I wrote a simple post which talks about the KNN algorithm.
The question is how to use this KV database in the model inference phrase. Let’s use the $x$ to denote the LLM’s input.
- Feed the $x$ into the LLM and get its vector representation $f(x)$.
- Use the KNN algorithm to get the $k$ nearest neighbors (denoted as $\mathcal N$) in the KV database using $f(x)$ as the query. To put it another way, find the most similar contexts for LLM’s input $x$. Note that each context has the corresponding next token.
- Let’s use $d_i$ to represents the distance between neighbor $i$ to $f(c)$. With $k$ neighbors we got a distance vector $[d_1, d_2,…,d_k]$. By negating the distances vector and applying the Softmax function, a probability distribution is obtained. This represents a probability distribution over distances but can also be converted into a probability distribution over the token $w_i$ corresponding to each neighbor $[p_1,p_2, p_3,…,p_k]$。Note that different neighbors may have the same next token, that is, $w_i=w_j (i\ne j)$ may be satisfied for some cases. Then we need to aggregate the probabilities (See the figure mentioned earlier, there are two Hawaii).
- Now we can set the probabilities of other tokens in the Vocab $\mathcal V$ to 0, which results in a probability distribution $p_\texttt{kNN}(y|x)$ over the Vocab $\mathcal V$, represents as a vector of length $|\mathcal V|$.
Note that the LLM also gives us a probability distribution $p_\texttt{LM}(y|x)$ over the Vocab $\mathcal V$ for the next token prediction.
Let’s use a hyper-parameter $\lambda$ to interploate these two distribution
$$ p(y|x)=\lambda p_\texttt{kNN}(y|x)+(1-\lambda)p_\texttt{LM}(y|x) $$
Experiments
The authors use FAISS for retrieving $k$ nearest neighbors fastly.
As for the measurement of the distance, the author mentioned that using Euclidean distance is better compared to the inner product distance.
The result of the Experiments says.
| Findings | Src |
|---|---|
| the $k\texttt{NN-LM}$ can improve the perplexity when using the KV database created from the same training data which is used to train the LM | Table 1 |
| Retrieving nearest neighbors from the corpus outperforms training on it | Table 3 |
| The best vector representation for context is the input of the FFN layer of the last transformer layer of LLM | Figure 3 |
| The higher the $k$, the lower the perplexity | Figure 4 |
| If the corpus for retrieving comes from the same domain, set $\lambda$ to a smaller value; otherwise, choose a large value | Figure 5 |
Pros and Cons
Now we are familiar with the mechanism of the $k\texttt{NN-LM}$ model, we can try to summarize the pros and cons.
Pros 1
- The $k\texttt{NN-LM}$ can capture some rare pattern and perform bettern on out-of-domain data. Because
- The $k\texttt{NN}$ part can handle such a case: The meaning of tokens is different even if they are the same and the context is similar.
- The $\texttt{LM}$ part can handle such a case: The next tokens are the same for different contexts.
Cons 1
- The KV database is space-expensive because we are creating KV pairs for each token, which is much more costly compared to creating text chunks in other RAG techniques. The Scalability of $k\texttt{NN-LM}$ is the main concern.
- There is no cross-attention between the model input and the retrieval result, which makes the model less expressive.