什么是 LoRA
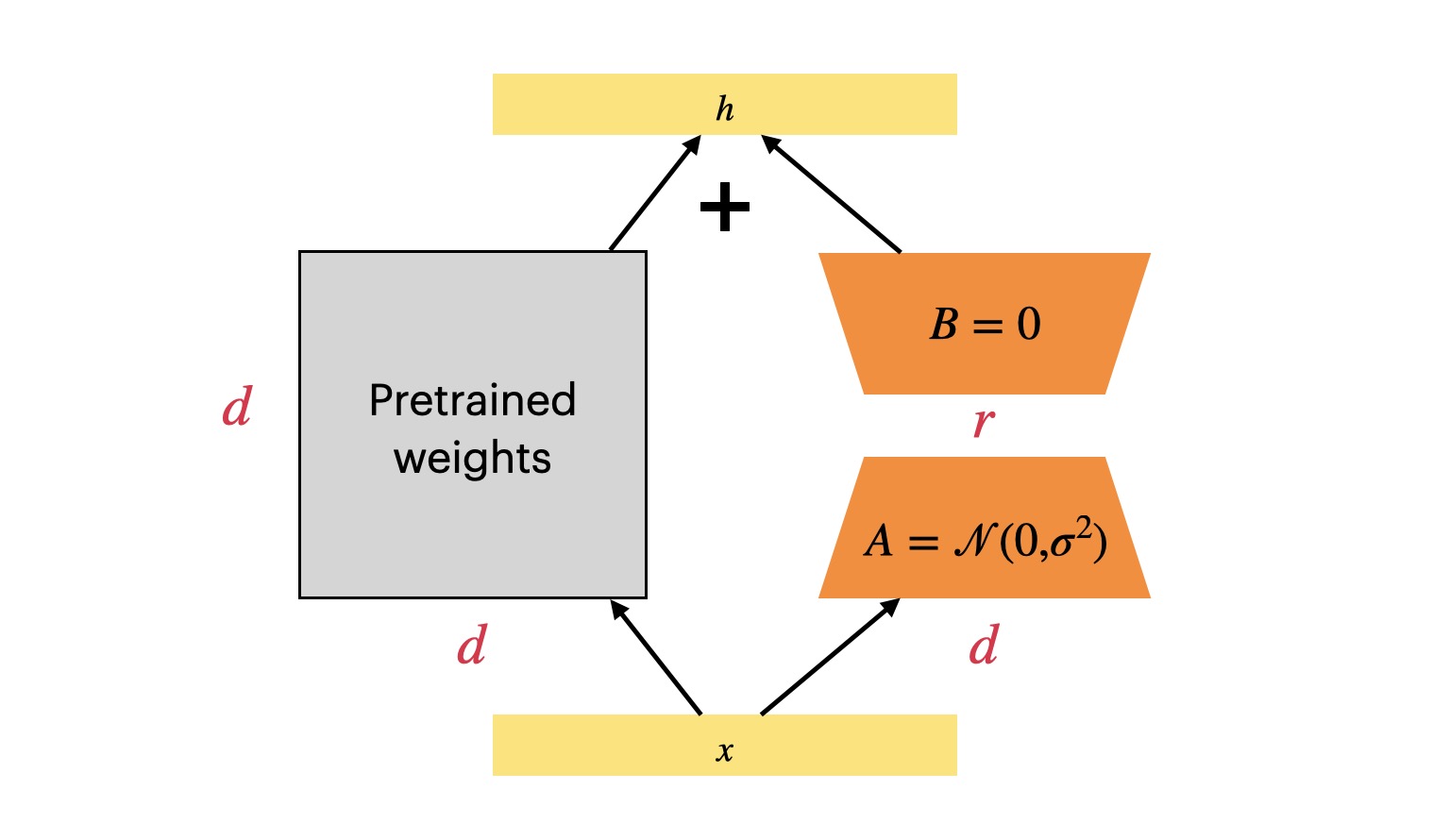
自从 LLM 时代到来之后,如何微调 LLM 成为了一个难题,因为 LLM 的模型实在是太大了,很难做全量微调更新所有参数。可选的路线有:冻结整个模型做 Prompt tuning 或者 In-context Learning;冻结整个模型但是会插入可训练的模块。今天要介绍的 LoRA(Low-Rank Adaptation) 就对应了后者的技术路线,这是微软团队的工作1

自从 LLM 时代到来之后,如何微调 LLM 成为了一个难题,因为 LLM 的模型实在是太大了,很难做全量微调更新所有参数。可选的路线有:冻结整个模型做 Prompt tuning 或者 In-context Learning;冻结整个模型但是会插入可训练的模块。今天要介绍的 LoRA(Low-Rank Adaptation) 就对应了后者的技术路线,这是微软团队的工作1
在 NLP 里面,一个核心的问题是,如何对文本进行分词?从分类的角度上面来说,可以分为:
先看 Char level 分词,顾名思义,就是把文本拆分成一个个字符单独表示,比如 highest -> h, i, g, h, e, s, t,一个显然的好处是,Vocab 不会太大,Vocab 的大小为字符集的大小,也不会遇到 Out-of-vocabulary(OOV) 的问题,但是字符本身并没有传达太多的语义,而且分词之后会有太多的 token,光是一个 highest 就可以得到 7 个 token,难以想象很长的文本分出来会有多少个😨